题目内容
6.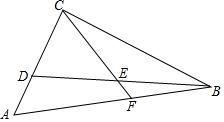 已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.
已知:如图,在Rt△ABC中,∠ACB=90°,点D在边AC上,点E是BD的中点,CE的延长线交边AB于点F,且∠CED=∠A.(1)求证:AC=AF;
(2)在边AB的下方画∠GBA=∠CED,交CF的延长线于点G,联结DG,在图中画出图形,并证明四边形CDGB是矩形.
分析 (1)只要证明∠CDE=∠ECD,∠CDE=∠AFC即可解决问题.
(2)只要证明CG=BD,CE=EG,DE=EB即可.
解答 (1)证明:∵∠BCD=90°,DE=EB,
∴EC=ED=EB,
∴∠EDC=∠ECD,
∵∠CED+∠CDE+∠DCE=180°,∠A+∠DCE+∠AFC=180°,
又∵∠CED=∠A,
∴∠CDE=∠AFC,
∴∠AFC=∠ACF,
∴AC=AF.
(2)解:图象如图所示.
∵∠CED=∠ABG,∠CED=∠A,
∴∠A=∠ABG,
∴AC∥BG,
∴∠ECD=∠BGE,
在△CED和△GEB中,
$\left\{\begin{array}{l}{∠DCE=∠BGE}\\{∠CED=∠GEB}\\{DE=EB}\end{array}\right.$,
∴△CED≌△GEB,
∴CE=EG,
∴CE=DE=EB,
∴CG=BD,CE=EG,DE=EB,
∴四边形CDGB是平行四边形,∵BD=CG,
∴四边形CDGB是矩形.
点评 本题考查矩形的性质、全等三角形的判定和性质、直角三角形斜边中线的性质、等腰三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,正确寻找全等三角形解决问题,属于中考常考题型.

练习册系列答案
相关题目
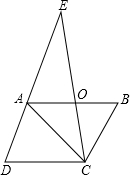
 已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
已知:如图,以矩形ABCD的对角线AC的中点O为圆心,OA长为半径作⊙O,过点B作BK⊥AC,垂足为K,过D作DH∥KB,DH分别与AC,AB,⊙O及CB的延长线相交于点E,F,G,H,且F是EG的中点.
 如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.
如图,△ABC中,∠B=58°,AB∥CD,∠ADC=∠DAC,∠ACB的平分线交DA的延长线于点E,则∠E的度数为29°.