题目内容
16.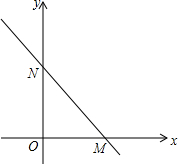 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.(1)求M,N两点的坐标;
(2)若点P在坐标轴上,且P到直线y=-$\frac{4}{3}$x+4的距离为$\frac{12}{5}$,求符合条件的P点坐标.
分析 (1)根据函数解析式,分别令x=0、y=0可以求得点N、M在坐标轴上的坐标;
(2)利用面积法来求点P的坐标.注意要分点P的坐标为(x,0)或(0,y)两种情况进行讨论.
解答 解:(1)令x=0,则y=4;
令y=0,则-$\frac{4}{3}$x+4=0,
解得x=3.
所以,N(0,4),M(3,0);
(2)由(1)知,N(0,4),M(3,0),则MN=5.
设P(x,0)或P(0,y).
①当点P的坐标为(x,0)时,$\frac{1}{2}$MN•$\frac{12}{5}$=$\frac{1}{2}$|x-3|•ON,即$\frac{1}{2}$×5×$\frac{12}{5}$=$\frac{1}{2}$|x-3|×4,
解得 x=0或x=6,
即P(0,0)或P(6,0);
②当点P的坐标为(0,y)时,$\frac{1}{2}$MN•$\frac{12}{5}$=$\frac{1}{2}$|y-4|•OM,即$\frac{1}{2}$×5×$\frac{12}{5}$=$\frac{1}{2}$|y-4|×3,
解得y=0或y=8,
即P(0,0)或P(0,8);
综上所述,符合条件的点P的坐标是(0,0)或(6,0)或(0,8).
点评 本题考查了一次函数图象上点的坐标特征.解答(2)题时,要分类讨论,以防漏解.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目
6.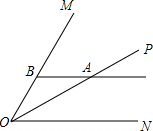 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
1.直线y=kx(k>0)与双曲线y=$\frac{2}{x}$交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则(x1-x2)(y1-y2)的值为( )
| A. | -4 | B. | 0 | C. | 4 | D. | 8 |
8. 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
 如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )
如图,直线a∥b,直线a⊥c,若∠1=70°,则∠2=( )| A. | 70° | B. | 90° | C. | 20° | D. | 80° |
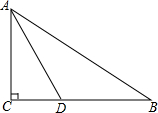 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D. 如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$. 如图,ABCD是正方形,E是BC边的中点,点F是EC边的中点,判断∠AFE与∠BAE的关系,并证明你的结论.
如图,ABCD是正方形,E是BC边的中点,点F是EC边的中点,判断∠AFE与∠BAE的关系,并证明你的结论.