题目内容
11. 如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
如图,AB半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE.设∠BEC=α,则tanα的值为$\frac{3}{2}$.
分析 首先连接BC,由AB半圆的直径,可得∠C=90°,然后由勾股定理求得BC的长,又由OD⊥AC,利用垂径定理可求得CE的长,继而求得答案.
解答 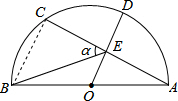 解:连接BC,
解:连接BC,
∵AB半圆的直径,OA=5,
∴∠C=90°,AB=2OA=10,
∵弦AC=8,
∴BC=$\sqrt{A{B}^{2}-A{C}^{2}}$=6,
∵OD⊥AC,
∴CE=$\frac{1}{2}$AC=4,
∴tanα=$\frac{BC}{CE}$=$\frac{6}{4}$=$\frac{3}{2}$.
故答案为:$\frac{3}{2}$.
点评 此题考查了圆周角定理、垂径定理、勾股定理以及三角函数等知识.注意准确作出辅助线是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱柱 |
 如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.
如图,抛物线y=x2-2x-3与x轴交A、B两点(A点在B点左侧),直线l与抛物线交于A、C两点,其中C点的横坐标为2.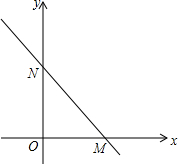 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.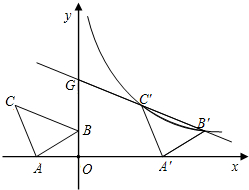 如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).
如图,在平面直角坐标系中有Rt△ABC,∠A=90°,AB=AC,A(-2,0)、B(0,d)、C(-3,2).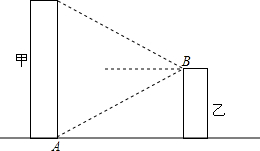 某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.
某城市搞亮化工程,如图,在甲楼底部,乙楼顶部分别安装一盏射灯.已知A灯恰好照到B灯,B灯恰好照到甲楼的顶部,如果两盏灯的光线与水平线的夹角相等,那么能否说甲楼的高度是乙楼的2倍?说说你的看法.