题目内容
6. 如图,ABCD是正方形,E是BC边的中点,点F是EC边的中点,判断∠AFE与∠BAE的关系,并证明你的结论.
如图,ABCD是正方形,E是BC边的中点,点F是EC边的中点,判断∠AFE与∠BAE的关系,并证明你的结论.
分析 设正方形边长是4a,根据三角函数中的正切值得出其关系即可.
解答 解:∠AFE=2∠BAE,
设正方形边长是4a,
可得BE=2a,BF=3a,
所以tan∠AFE=$\frac{AB}{BF}=\frac{4a}{3a}=\frac{4}{3}$,
tan∠BAE=$\frac{BE}{AB}=\frac{2a}{4a}=\frac{1}{2}$,
因为tan26.5°≈$\frac{1}{2}$,tan53°≈$\frac{4}{3}$,
所以可得:∠AFE=2∠BAE.
点评 此题考查正方形的性质,关键是根据正方形的性质设出边长,再利用三角函数值得出角的关系.

练习册系列答案
相关题目
11. 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
 如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )
如图,四边形ABCD和四边形AEFC是两个平行四边形,点B在EF边上,若平行四边形ABCD和平行四边形AEFC的面积分别是s1,s2,则它们的大小关系是( )| A. | s1>s2 | B. | 2s1<s2 | C. | s1<s2 | D. | s1=s2 |
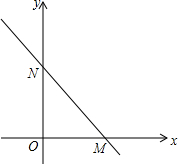 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.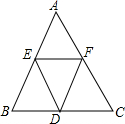 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?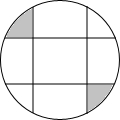 如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.
如图,圆中有四条弦,每一条弦都将圆分割成面积比为1:3的两个部分,若这些弦的交点恰是一个正方形的顶点,那么这个正方形的外接圆的面积与图中阴影部分面积的比值为π.