题目内容
4.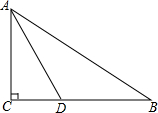 如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.
如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于点D.(1)以AB边上一点O为圆心,过A,D两点作⊙O(不写作法,保留作图痕迹);
(2)判断直线BC与⊙O的位置关系,并说明理由;
(3)若(1)中的⊙O与边AB的另一个交点为E,AB=6,BD=2$\sqrt{3}$,求弧DE的弧长(结果保留根号和π)
分析 (1)作出AD的垂直平分线交AB于点O,以O为圆心,OA为半径作圆即可;
(2)利用等腰三角形的性质和角的平分线的性质求得OD∥AC. 进而求出∠ODB=90°,从而得出BC为⊙O的切线.
(3)设⊙O的半径为r,则OB=6-r,在RT△ODB中,根据勾股定理求得r的值,进而根据已知求得∠DOB=60°,然后根据弧长公式求得即可.
解答 解:(1)如图,作AD的垂直平分线交AB于点O,以O为圆心,OA为半径作圆;
(2)直线BC与⊙O相切.
理由如下: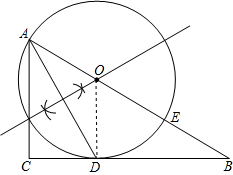
连接OD,
∵OA=OD,
∴∠OAD=∠ODA.
∵AD平分∠BAC,
∴∠OAD=∠DAC.
∴∠ODA=∠DAC.
∴OD∥AC.
∵∠C=90°,
∴∠ODB=90°,
即OD⊥BC.
∴BC为⊙O的切线.
(3)设⊙O的半径为r,则OB=6-r,
在RT△ODB中,∠ODB=90°,
∴OB2=OD2+BD2,即(6-r)2=r2+(2$\sqrt{3}$)2,
解得r=2,
∴OB=4,
∴∠OBD=30°,∠DOB=60°,
∴l=$\frac{60π×2}{180}$=$\frac{2}{3}$π,
∴弧DE的弧长$\frac{2}{3}$π.
点评 此题主要考查了复杂作图、切线的判定、勾股定理的应用以及弧长的计算,利用角平分线的性质得出OD∥AC是解题关键.

练习册系列答案
相关题目
12.一元二次方程(1-k)x2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<2且k≠1 | B. | k>2且k≠1 | C. | k>2 | D. | k<2 |
 如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点
如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点 已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).
已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0). 如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.
如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.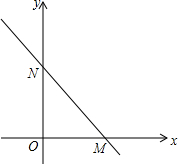 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N. 请从以下两小题中任选一个作答,若多选,则按所选的第一题计分
请从以下两小题中任选一个作答,若多选,则按所选的第一题计分