题目内容
1.直线y=kx(k>0)与双曲线y=$\frac{2}{x}$交于A,B两点,若A,B两点的坐标分别为A(x1,y1),B(x2,y2),则(x1-x2)(y1-y2)的值为( )| A. | -4 | B. | 0 | C. | 4 | D. | 8 |
分析 求出两函数组成的方程组的解,代入即可求出答案.
解答 方法一:
解:∵解$\left\{\begin{array}{l}{y=kx}\\{y=\frac{2}{x}}\end{array}\right.$得:$\left\{\begin{array}{l}{{x}_{1}=\frac{\sqrt{2k}}{k}}\\{{y}_{1}=\sqrt{2k}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\frac{\sqrt{2k}}{k}}\\{{y}_{2}=-\sqrt{2k}}\end{array}\right.$,
∴(x1-x2)(y1-y2)的值为($\frac{\sqrt{2k}}{k}$+$\frac{\sqrt{2k}}{k}$)($\sqrt{2k}$+$\sqrt{2k}$)
=$\frac{2\sqrt{2k}}{k}$×2$\sqrt{2k}$
=8.
方法二:
解:∵直线y=kx(k>0)与双曲线y=$\frac{2}{x}$交于A,B两点,
∴A、B两点关于原点对称,
∴x1=-x2,y1=-y2
∴(x1-x2)(y1-y2)=x1y1-x1y2-x2y1+x2y2=2x1y1+2x2y2=4+4=8,
故选D.
点评 本题考查了一次函数与反比例函数的交点问题的应用,主要考查学生的计算能力.

练习册系列答案
相关题目
12.一元二次方程(1-k)x2-2x-1=0有两个不相等的实数根,则k的取值范围是( )
| A. | k<2且k≠1 | B. | k>2且k≠1 | C. | k>2 | D. | k<2 |
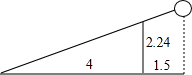 已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米.
已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米. 如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.
如图,直线l∥m∥n,等边△ABC的顶点B,C分别在直线n和m上,边BC与直线n所夹的角为25°,则∠α的度数为35度.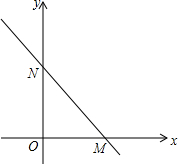 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
 请从以下两小题中任选一个作答,若多选,则按所选的第一题计分
请从以下两小题中任选一个作答,若多选,则按所选的第一题计分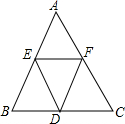 如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?
如图所示,AB=BC=CA=2,将△ABC的三边均分为二等分,并按图中那样构成,则图中有几个三角形?请用你手中的刻度尺度量一下,它们分别是什么形状的三角形?