��Ŀ����
7����������y=mx2-3mx+2��m��0����x��Ľ���ΪA��x1��0����B��x2��0������x12+x22=17������x1�� x2����P��a��b��Ϊ��������һ���㣮��1���������ߵĽ���ʽ��
��2������AC����P����ֱ��PE��AC��x���ڵ�E����y���ڵ�F��O��t������aȡ��ֵʱt�����ֵ�����ֵ�Ƕ��٣�
��3���ж��ڣ�2�����������Ƿ����һ��P��ʹ�Ե�A��C��P��EΪ������ı���Ϊƽ���ı��Σ�����������˵�����ɣ������ڣ��������P�����꣮
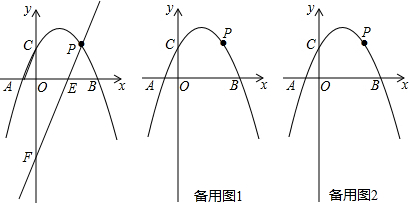
���� ��1���ȸ���������y=mx2-3mx+2��m��0����x��Ľ���ΪA��x1��0����B��x2��0����֪x1��x2Ϊ���̵������������ɸ���ϵ���Ĺ�ϵ���ɵó�m��ֵ��
��2�������A��B��������꣬�����ô���ϵ�������ֱ��AC�Ľ���ʽ����ֱ��PE��AC������F��0��t����ֱ֪��PE�Ľ���ʽΪy=2x+t�����ݵ�P��a��b��Ϊֱ���������ߵĽ���ɵó�����a��t�Ķ��κ�������ʽ�����t�����ֵ���ɣ�
��3���ٵ���Pλ��x���Ϸ�ʱ��������ԳƵ����ʿɵó�P�����ꣻ
�ڵ���Pλ��x���·�ʱ������CE��AP����PM��x���ڵ�M���ı���ACEP��ƽ���ı��οɵó���COE�ա�PMA����PM=OC=2��P���������Ϊ-2�����������ߵĽ���ʽ���ɵó�x��ֵ�������ó�P�����꣮
��� �⣺��1���ߵ�������y=mx2-3mx+2��m��0����x���ཻʱ��y=0����mx2-3mx+2=0��?????
��x1��x2Ϊ���̵���������
��x1+x2=-$\frac{-3m}{m}$=3��x1x2=$\frac{2}{m}$��
�֡�x12+x22=17��
�ࣨx1+x2��2-2x1x2=17��
��9-$\frac{4}{m}$=17��????????
��m=-$\frac{1}{2}$��
�������ߵĽ���ʽΪy=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��2����y=-$\frac{1}{2}$x2+$\frac{3}{2}$x+2����y=0ʱ��$\frac{1}{2}$x2+$\frac{3}{2}$x+2=0��
��ã�x1=-1��x2=4��????????????????????????
��A��-1��0����B��4��0��
��x=0ʱ��y=2��
��C��0��2��
��ֱ��AC�Ľ���ʽΪ��y=kx+b
��A��B����������ʽ$\left\{\begin{array}{l}b=2\\-k+b=0\end{array}\right.$�����$\left\{\begin{array}{l}k=2\\ b=2\end{array}\right.$��
��ֱ��PE��AC������F��0��t��
��ֱ��PE�Ľ���ʽΪ y=2x+t
�ߵ�P��a��b��Ϊֱ���������ߵĽ��㣬
��$\left\{\begin{array}{l}-\frac{1}{2}{a}^{2}+\frac{3}{2}a+2=b\\ 2a+t=b\end{array}\right.$��?
��t=-$\frac{1}{2}$a2-$\frac{1}{2}$a+2
=-$\frac{1}{2}$��a+$\frac{1}{2}$��2+$\frac{17}{8}$��$\frac{17}{8}$��
�൱a+$\frac{1}{2}$=0����a=-$\frac{1}{2}$ʱ��t���ֵΪ$\frac{17}{8}$��
????????????????????????????????????????
��3���⣺���������ĵ�P�� ����ͼ1������Pλ��x���Ϸ�ʱ��
����ͼ1������Pλ��x���Ϸ�ʱ��
��PC��AE��
��PC��x�ᣬ
���C���P���������ߵĶԳ���Գƣ�
�������ߵĶԳ���Ϊx=$\frac{3}{2}$��C��0��2����
��P��3��2����
����ͼ2������Pλ��x���·�ʱ��
CE��AP����PM��x���ڵ�M��
���ı���ACEP��ƽ���ı��Σ�
��AC��PE��AC=PE�� ��$\left\{\begin{array}{l}��COE=��PMA\\��APM=��ECO\\ PE=CE\end{array}\right.$��
��$\left\{\begin{array}{l}��COE=��PMA\\��APM=��ECO\\ PE=CE\end{array}\right.$��
���COE�ա�PMA��AAS����
��PM=OC=2
��P���������Ϊ-2�����������ߵĽ���ʽ
y=$\frac{1}{2}$x2+$\frac{3}{2}$x+2��
��$\frac{1}{2}$x2+$\frac{3}{2}$x+2=-2��??????????????
���x=$\frac{3��\sqrt{41}}{2}$��???????????????
��P��$\frac{3+\sqrt{41}}{2}$��-2����$\frac{3-\sqrt{41}}{2}$��-2����???
��ʹ�Ե�A��C��P��EΪ������ı���Ϊƽ���ı��ε�P������������3��2������$\frac{3+\sqrt{41}}{2}$��-2������$\frac{3-\sqrt{41}}{2}$��-2����?
���� ���⿼����Ƕ��κ����ۺ��⣬�漰�����κ���ͼ���ϵ�������ص㡢����ϵ���Ĺ�ϵ��ƽ���ı��ε��ж������ʵ�֪ʶ���ѶȽϴ�

 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�| A�� | k��2��k��1 | B�� | k��2��k��1 | C�� | k��2 | D�� | k��2 |
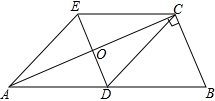 ��ͼ����ABC�У���BCA=90�㣬CD�DZ�AB�ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���߽��ڵ�E����DE��AC�ڵ�O������AE��
��ͼ����ABC�У���BCA=90�㣬CD�DZ�AB�ϵ����ߣ��ֱ����C��D��BA��BC��ƽ���߽��ڵ�E����DE��AC�ڵ�O������AE�� ��֪������x��һԪ���η���-x2+��m+1��x+��m+2��=0��m��0����
��֪������x��һԪ���η���-x2+��m+1��x+��m+2��=0��m��0����
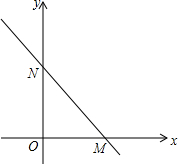 ��ͼ��ֱ��y=-$\frac{4}{3}$x+4��������ֱ��ڵ�M��N��
��ͼ��ֱ��y=-$\frac{4}{3}$x+4��������ֱ��ڵ�M��N��