题目内容
6.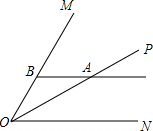 如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )
如图,已知∠MON=60°,OP是∠MON的角平分线,点A是OP上一点,过点A作ON的平行线交OM于点B,AB=4.则直线AB与ON之间的距离是( )| A. | $\sqrt{3}$ | B. | 2 | C. | $2\sqrt{3}$ | D. | 4 |
分析 过A作AC⊥OM,AD⊥ON,由OP为角平分线,利用角平分线定理得到AC=AD,AD即为直线AB与ON之间的距离,由BA与ON平行得到一对内错角相等,再由角平分线得到一对角相等,等量代换得到一对角相等,再利用外角性质及直角三角形的性质得到∠BAC=30°,利用30度角所对的直角边等于斜边的一半求出BC的长,利用勾股定理求出AC的长,即为AD的长.
解答 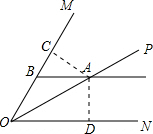 解:过A作AC⊥OM,AD⊥ON,
解:过A作AC⊥OM,AD⊥ON,
∵OP平分∠MON,∠MON=60°,
∴AC=AD,∠MOP=∠NOP=30°,
∵BA∥ON,
∴∠BAO=∠PON=30°,
∵∠ABC为△AOB的外角,
∴∠ABC=60°,
在Rt△ABC中,∠BAC=30°,AB=4,
∴BC=2,
根据勾股定理得:AC=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴AD=AC=2$\sqrt{3}$,
则直线AB与ON之间的距离为2$\sqrt{3}$,
故选C.
点评 此题考查了勾股定理,含30度直角三角形的性质,以及平行线的性质,熟练掌握勾股定理是解本题的关键.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
1. 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )
 一个几何体的三视图如图所示,则这个几何体是( )
一个几何体的三视图如图所示,则这个几何体是( )| A. | 圆柱 | B. | 球 | C. | 圆锥 | D. | 棱柱 |
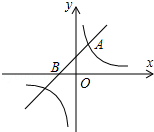 如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).
如图,一次函数y=x+1的图象与反比例函数$y=\frac{k}{x}$(k为常数,且k≠0)的图象都经过点A(m,2).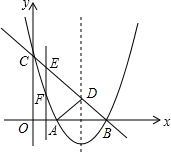 如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点
如图,某抛物线顶点坐标为(2,-1)与y轴交于点C(0,3),与x轴交于A、B两点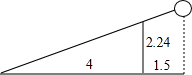 已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米.
已知女排赛场球网的高度是2.24米,某排球运动员在一次扣球时,球恰好擦网而过,落在对方场地距离球网4米的位置上,此时该运动员距离球网1.5米,假设此次排球的运行路线是直线,则该运动员击球的高度是3.08米.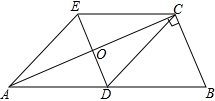 如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE.
如图,△ABC中,∠BCA=90°,CD是边AB上的中线,分别过点C,D作BA,BC的平行线交于点E,且DE交AC于点O,连接AE. 已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).
已知:关于x的一元二次方程-x2+(m+1)x+(m+2)=0(m>0).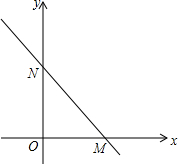 如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.
如图,直线y=-$\frac{4}{3}$x+4与坐标轴分别交于点M、N.