题目内容
 已知,在△ABC中,分别以AB,AC为斜边作等腰直角三角形ABM和CAN,P是边BC的中点,求证:PM=PN.
已知,在△ABC中,分别以AB,AC为斜边作等腰直角三角形ABM和CAN,P是边BC的中点,求证:PM=PN.考点:三角形中位线定理,全等三角形的判定与性质,直角三角形斜边上的中线
专题:证明题
分析:如图你作辅助线;首先证明MD=PQ、PD=NQ,∠MDP=∠PQN,然后运用SAS公理证明△MDP≌△PQN,即可解决问题.
解答: 解:如图,分别取AB、AC的中点D、Q;
解:如图,分别取AB、AC的中点D、Q;
连接DM、DP;QN、QP;
∵点P为BC的中点,
∴DP∥AC,DP=
AC;同理可证:
PQ∥AB,PQ=
AB;
∴∠BDP=∠PQC=∠BAC(设为α);
∵△ABM、△ACN均为等腰直角三角形,
且D、Q均为AB、AC的中点,
∴MD=
AB,NQ=
AC,∠MDB=∠NQC=90°,
∴MD=PQ、PD=NQ,∠MDP=∠PQN=90°-α;
在△MDP与△PQN中,
,
∴△MDP≌△PQN(SAS),
∴PM=PN.
 解:如图,分别取AB、AC的中点D、Q;
解:如图,分别取AB、AC的中点D、Q;连接DM、DP;QN、QP;
∵点P为BC的中点,
∴DP∥AC,DP=
| 1 |
| 2 |
PQ∥AB,PQ=
| 1 |
| 2 |
∴∠BDP=∠PQC=∠BAC(设为α);
∵△ABM、△ACN均为等腰直角三角形,
且D、Q均为AB、AC的中点,
∴MD=
| 1 |
| 2 |
| 1 |
| 2 |
∴MD=PQ、PD=NQ,∠MDP=∠PQN=90°-α;
在△MDP与△PQN中,
|
∴△MDP≌△PQN(SAS),
∴PM=PN.
点评:该题主要考查了全等三角形的判定及其性质、三角形的中位线定理、直角三角形的性质等几何知识点及其应用问题;解题的关键是作辅助线,灵活运用全等三角形的判定及其性质、三角形的中位线定理等来分析、判断、解答.

练习册系列答案
 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案
相关题目
点p(5.-3)关于原点对称的点的坐标是( )
| A、(3,-5) |
| B、(-5,-3) |
| C、(-5,3) |
| D、(-3,5) |
下列图形中既是轴对称,又是中心对称的是( )
A、 |
B、 |
C、 |
D、 |
“两次抛一枚均匀的骰子,两次朝上面的点数之和为1”,这一事件是( )
| A、必然事件 | B、随机事件 |
| C、确定事件 | D、不可能事件 |
某校九年级开展“光盘行动”宣传活动,各班级参加该活动的人数统计结果如下表,对于这组统计数据,下列说法中正确的是( )
| 班级 | 1班 | 2班 | 3班 | 4班 | 5班 | 6班 |
| 人数 | 52 | 60 | 62 | 54 | 58 | 62 |
| A、极差是40 |
| B、众数是60 |
| C、平均数是58 |
| D、中位数是58 |
 如图,已知在三角形ABC中,AB>AC,AD是边上的高,求证:AB2-AC2=BC(BD-CD).
如图,已知在三角形ABC中,AB>AC,AD是边上的高,求证:AB2-AC2=BC(BD-CD). 四边形ABCD中,AB=
四边形ABCD中,AB=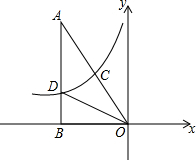 如图,Rt△OAB与曲线y1=
如图,Rt△OAB与曲线y1=