题目内容
在△ABC中,AB=2
,△ABC外接圆的半径为2,则∠C= 度.
| 3 |
考点:圆周角定理,垂径定理,特殊角的三角函数值
专题:
分析:根据题意画出图形,有两种情况:①当∠C为锐角,②当∠C为钝角,连接AO并延长交于圆于点D,连接BD.所以∠ABD=90°,∠ADB=∠ACB,则sin∠D=
=
=
,进而求得角度.
| AB |
| AD |
2
| ||
| 4 |
| ||
| 2 |
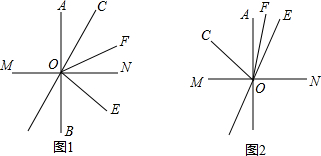
解答:解:由题意如图1,
连接AO并延长交于圆于点D,连接BD,

∴∠ABD=90°,∠ADB=∠ACB
则sin∠D=
=
=
,
∴∠D=60°,
即∠C=60°;
如图2,

由图可知:∠C与∠D互补,
由①知∠D=60°,
所以∠C=120°,
故∠C=60°或120°.
故答案为:60或120.
连接AO并延长交于圆于点D,连接BD,

∴∠ABD=90°,∠ADB=∠ACB
则sin∠D=
| AB |
| AD |
2
| ||
| 4 |
| ||
| 2 |
∴∠D=60°,
即∠C=60°;
如图2,

由图可知:∠C与∠D互补,
由①知∠D=60°,
所以∠C=120°,
故∠C=60°或120°.
故答案为:60或120.
点评:本题考查了有关三角形以及外接圆问题,本题主要利用直径所对的圆周角为直角,另外注意分两种情况.

练习册系列答案
相关题目
下列图形中既是轴对称,又是中心对称的是( )
A、 |
B、 |
C、 |
D、 |
“两次抛一枚均匀的骰子,两次朝上面的点数之和为1”,这一事件是( )
| A、必然事件 | B、随机事件 |
| C、确定事件 | D、不可能事件 |
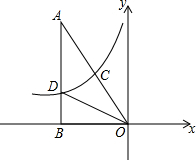 如图,Rt△OAB与曲线y1=
如图,Rt△OAB与曲线y1=
 如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由.
如图,在△ABC中,∠C=90°,AD是∠BAC的平分线,过点D作DE⊥AB.DE恰好是∠ADB的平分线.CD与DB有怎样的数量关系?请说明理由.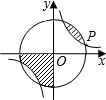 如图,已知点P(3a,a)是反比例函数y=
如图,已知点P(3a,a)是反比例函数y= 如图,直线l1:y=k1x+b与直线l2:y=k2x交于点(-1,3),则关于x的不等式k2x>k1x+b的解集为
如图,直线l1:y=k1x+b与直线l2:y=k2x交于点(-1,3),则关于x的不等式k2x>k1x+b的解集为