题目内容
6.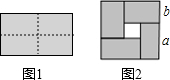 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
分析 先求出正方形的边长,继而得出面积,然后根据空白部分的面积=正方形的面积-矩形的面积即可得出答案.
解答 解:∵图(1)是一个长为2a,宽为2b(a>b)的长方形,
∴正方形的边长为:a+b,
∵由题意可得,正方形的边长为(a+b),
正方形的面积为(a+b)2,
∵原矩形的面积为4ab,
∴中间空的部分的面积=(a+b)2-4ab=(a-b)2.
故选:D.
点评 此题考查了完全平方公式的几何背景,求出正方形的边长是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
16.在△ABC和△A′B′C′中,AB=A′B′,∠B=∠B′,补充条件后仍不一定能保证△ABC≌△A′B′C′( )
| A. | AB=B'C' | B. | ∠A=∠A′ | C. | AC=A′C′ | D. | ∠C=∠C′ |
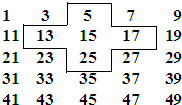 将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
将连续的奇数1,3,5,7,9,…,排成如图所示的数阵.
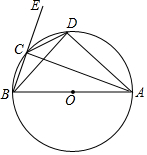 如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE
如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE 如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )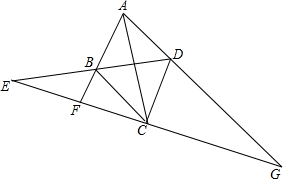 已知:如图,菱形ABCD,分别延长AB、DB、AD交直线EC于E、F、G,且AG=2AF,求证:EB=BD.
已知:如图,菱形ABCD,分别延长AB、DB、AD交直线EC于E、F、G,且AG=2AF,求证:EB=BD.