题目内容
18. 如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )
如图,在△ABC中,点D,E分别在边AB、AC上,DE∥BC.已知AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,则AC的长等于( )| A. | 8 | B. | 21 | C. | 14 | D. | 7 |
分析 根据平行线分线段成比例定理得到$\frac{AD}{DE}$=$\frac{AE}{EC}$,则利用比例性质可求出EC,然后计算AE+EC即可.
解答 解:∵DE∥BC.
∴$\frac{AD}{DE}$=$\frac{AE}{EC}$,
而AE=6,$\frac{AD}{DB}$=$\frac{3}{4}$,
∴$\frac{6}{EC}$=$\frac{3}{4}$,
∴EC=8,
∴AC=AE+EC=6+8=14.
故选C.
点评 本题考查了平行线分线段成比例定理:三条平行线截两条直线,所得的对应线段成比例.

练习册系列答案
相关题目
6.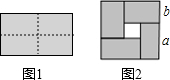 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
7.如果a2=(-3)2,那么a等于( )
| A. | 3 | B. | -3 | C. | 9 | D. | ±3 |

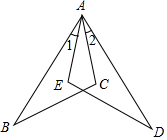 如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可)
如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可)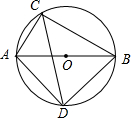 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D. 如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
如图,一次函数y=kx+b与反比例函数y=$\frac{a}{x}$在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.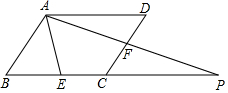 在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.
在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.