题目内容
1.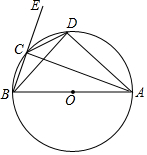 如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE
如图,已知AB是⊙O的直径,C、D均在⊙O上,点E在BC的延长线上,CD平分∠ACE(1)求∠DBA的度数;
(2)求证:BD=AD.
分析 (1)根据圆周角定理求得∠ADB=90°,∠ACD=∠DAB,根据圆内接四边形的性质求得∠DCE=∠DAB,进而求得∠DBA=∠DAB=45°.
(2)根据等角对等边即可证得.
解答 (1)解:∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠DCE=∠DAB,∠DCE=∠ACD,
∴∠ACD=∠DAB,
∵∠DBA=∠ACD,
∴∠DBA=∠DAB=45°.
(2)证明:∵∠DBA=∠DAB=45°.
∴BD=AD.
点评 本题考查了圆周角定理,圆内接四边形的性质,角平分线的性质,熟练掌握圆周角定理是解题的关键.

练习册系列答案
 新编小学单元自测题系列答案
新编小学单元自测题系列答案 字词句段篇系列答案
字词句段篇系列答案
相关题目
6.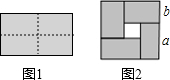 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
 如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )
如图1是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四块形状和大小都一样的小长方形,然后按图2那样拼成一个正方形,则中间空的部分的面积( )| A. | a2-b2 | B. | 2ab | C. | (a+b)2 | D. | (a-b)2 |
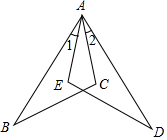 如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可)
如图所示,已知∠1=∠2,AC=AE,再添一个条件AB=AD或∠B=∠D或∠C=∠E,使△ABC≌△ADE.(只需写出一个即可)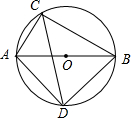 如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D.
如图,⊙O的直径AB的长为10,弦AC的长为5,∠ACB的平分线交⊙O于点D. 在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.
在?ABCD中,点E,F分别是BC,CD上的点,且DF=CF,连接AE,AF,并延长AF交BC的延长线于点P.