题目内容
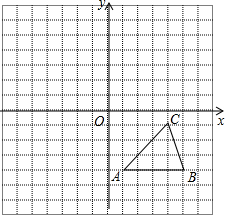 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).(1)把△ABC向上平移5个单位后得到对应的△A1B1C1,画出△A1B1C1,并写出C1的坐标;
(2)以原点O为对称中心,在画出与△A1B1C1关于原点O对称的△A2B2C2,并写出点C2的坐标;
(3)求出经过C1C2的直线表达式.
考点:作图-旋转变换,待定系数法求一次函数解析式,作图-平移变换
专题:
分析:(1)根据网格结构,找出点A、B、C向上平移5个单位的对应点A1、B1、C1的位置,然后顺次连接即可,再根据平面直角坐标系写出点C1的坐标;
(2)根据网格结构,找出点A1、B1、C1关于原点O的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点C2的坐标;
(3)设经过C1C2的直线表达式为y=kx+b,将C1、C2的坐标代入求出k和b的值,继而可求得解析式.
(2)根据网格结构,找出点A1、B1、C1关于原点O的对应点A2、B2、C2的位置,然后顺次连接即可,再根据平面直角坐标系写出点C2的坐标;
(3)设经过C1C2的直线表达式为y=kx+b,将C1、C2的坐标代入求出k和b的值,继而可求得解析式.
解答:解:(1)所作图形如图所示,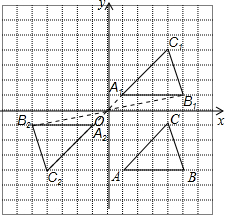
点C1的坐标为(4,4);
(2)所作图形如图所示,
点C2的坐标(-4,-4);
(3)设经过C1C2的直线表达式为y=kx+b,
由题意得,
,
解得:
,
则经过C1C2的直线表达式为y=x.

点C1的坐标为(4,4);
(2)所作图形如图所示,
点C2的坐标(-4,-4);
(3)设经过C1C2的直线表达式为y=kx+b,
由题意得,
|
解得:
|
则经过C1C2的直线表达式为y=x.
点评:本题考查了利用旋转变换作图,利用平移变换作图,熟练掌握网格结构,并准确找出对应点的位置是解题的关键.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
 已知二次函数y=-x2+2x+3图象的对称轴为直线.
已知二次函数y=-x2+2x+3图象的对称轴为直线.
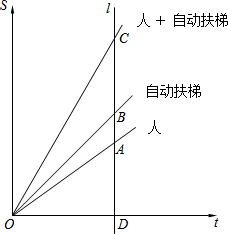 如图,直线l与x轴垂直,垂足为D,它与从原点出发的三条射线分别交于点A、B、C.射线OA、OB、OC分别表示正常行走的人,站在自动扶梯上不走的人,在自动扶梯上同时正常行走的人所移动的路程s(m)与时间t(min)的函数关系,在这些关系中,正常行走的人的速度相同,自动扶梯的速度也相同.
如图,直线l与x轴垂直,垂足为D,它与从原点出发的三条射线分别交于点A、B、C.射线OA、OB、OC分别表示正常行走的人,站在自动扶梯上不走的人,在自动扶梯上同时正常行走的人所移动的路程s(m)与时间t(min)的函数关系,在这些关系中,正常行走的人的速度相同,自动扶梯的速度也相同.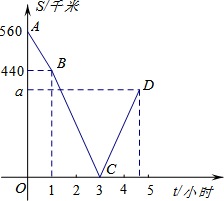 甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车才出发,并以各自速度匀速行驶,甲车出发3小时两车相遇,相遇后两车仍按原速度原方向各自行驶.如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间t(小时)之间的函数图象.则:
甲、乙两车分别从M、N两地相向而行,甲车出发1小时后乙车才出发,并以各自速度匀速行驶,甲车出发3小时两车相遇,相遇后两车仍按原速度原方向各自行驶.如图折线A-B-C-D表示甲、乙两车之间的距离S(千米) 与甲车出发时间t(小时)之间的函数图象.则: