题目内容
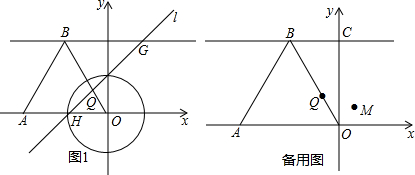
如图1,在平面直角坐标系中,等边△OAB的顶点A(-6,0),顶点B在第二象限,顶点O为坐标原点,过点B作BC∥OA交y轴于点C.
(1)填空:点B的坐标是 ;
(2)若点Q是线段OB上的一点,且OQ=
OB,过点Q作直线l分别与直线AO、
直线BC交于点H、G,以点O为圆心,OH的长为半径作⊙O.
①设点G的横坐标为x,当点G在直线BC上移动,试探究:当x为何值时,⊙O与直线BC、直线AB都分别相切?
②过点G作GD∥OC,交x轴于点D,若线段GD与⊙O有公共点P,且点M(1,1),探求:2PO+PM的最小值.
(1)填空:点B的坐标是
(2)若点Q是线段OB上的一点,且OQ=
| 1 |
| 3 |
直线BC交于点H、G,以点O为圆心,OH的长为半径作⊙O.
①设点G的横坐标为x,当点G在直线BC上移动,试探究:当x为何值时,⊙O与直线BC、直线AB都分别相切?
②过点G作GD∥OC,交x轴于点D,若线段GD与⊙O有公共点P,且点M(1,1),探求:2PO+PM的最小值.

考点:圆的综合题
专题:
分析:(1)由△OAB为等边三角形,且OB=6,所以BC=3,CO=3
,考虑象限中坐标的正负取值,结果易得.
(2)①分别相切,我们就把这种情形画出来,此时H点已知,Q点已知,连接HQ并延长,其与直线BC的交点记为G,根据三角形相关性质,G点的横坐标不难求出.
②2PO+PM,判定最值时我们一般首先把多倍的情况转化成某线段的长,因为这样比较起来更为直观,由上问可知
=
,又OH=OP,则易得2PO+PM=BG+PM.移动中发现,BG为平行于x轴的线段,且B点固定,有BG为B点到GD的距离,而PM不平行于x轴,若作辅助线有PM≥M到GD的距离.PM何时等于M到GD的距离呢?当G在y轴左边,存在情形如图4,M到GD距离=PM,则2PO+PM=B点到GD的距离+M到GD的距离=B点横坐标-M点横坐标.且B、M点固定,则最小距离易求.
| 3 |
(2)①分别相切,我们就把这种情形画出来,此时H点已知,Q点已知,连接HQ并延长,其与直线BC的交点记为G,根据三角形相关性质,G点的横坐标不难求出.
②2PO+PM,判定最值时我们一般首先把多倍的情况转化成某线段的长,因为这样比较起来更为直观,由上问可知
| OH |
| BG |
| 1 |
| 2 |
解答:解:
(1)B(-3, 3
).
分析如下:

如图1,过点B作BC⊥AO于C,
∵△OAB为等边三角形,
∴C为中点,
∴CO=
•AO=3,
∵∠OCB=
∠OBA=30°,
∴BC=
•CO=3
,
∴B(-3,3
).
(2)
①

如图2,以O为圆心,OC的长为半径画圆,交AO于H,H',连接HQ并延长,交BC的延长线于G,H'Q并延长,交CB的延长线于G',
显然本题有两种情况.
∵△OAB是等边三角形,
∴O点到AB的距离=B点到AO的距离,
∵B点到AO的距离=OC=3
,
∴O点到AB的距离=3
,即⊙O与AB相切.
(i)
∵BC∥OA
∴
=
,
∵OQ=
OB,
∴
=
,
∵OH=OC=3
,
∴
=
=
,
解得 BG=6
,
∴CG=BG-BC=6
-3,
∴当x=6
-3时,⊙O与直线BC、直线AB都分别相切.
(ii)
∵BC∥OA
∴
=
,
∵OQ=
OB,
∴
=
,
∵OH′=OC=3
,
∴
=
=
,
解得 BG′=6
,
∴CG′=BG′+BC=6
+3,
∴当x=6
+3时,⊙O与直线BC、直线AB都分别相切.
综上所述,x=6
-3或x=-6
-3时⊙O与直线BC、直线AB都分别相切.
②

如图3,过点M作x轴的平行线l,交GD于N,
由①可得
=
,
∴
=
,
∴2OP+PM=BG+PM.
在Rt△PMN中,
∵PM≥MN(等号在P、N重合时成立)
∴2PO+PM=BG+PM≥BG+MN.
若移动G点至G'位置,此时N',P'重合,此时2PO+PM应最小.
显然G移动,H也跟着移动,圆的大小也发生变化,是否有P、N重合的情景呢?

如图4,在运动的过程中,存在情形使得P、N重合,此时BG+PM=M的横坐标-B的横坐标.
∵B(-3,3
),M(1,1),
∴2PO+PM=BG+PM=xM-xB=1-(-3)=4,
2PO+PM的最小值是4.
(1)B(-3, 3
| 3 |
分析如下:

如图1,过点B作BC⊥AO于C,
∵△OAB为等边三角形,
∴C为中点,
∴CO=
| 1 |
| 2 |
∵∠OCB=
| 1 |
| 2 |
∴BC=
| 3 |
| 3 |
∴B(-3,3
| 3 |
(2)
①

如图2,以O为圆心,OC的长为半径画圆,交AO于H,H',连接HQ并延长,交BC的延长线于G,H'Q并延长,交CB的延长线于G',
显然本题有两种情况.
∵△OAB是等边三角形,
∴O点到AB的距离=B点到AO的距离,
∵B点到AO的距离=OC=3
| 3 |
∴O点到AB的距离=3
| 3 |
(i)
∵BC∥OA
∴
| OH |
| BG |
| OQ |
| BQ |
∵OQ=
| 1 |
| 3 |
∴
| OQ |
| BQ |
| 1 |
| 2 |
∵OH=OC=3
| 3 |
∴
3
| ||
| BG |
| OQ |
| BQ |
| 1 |
| 2 |
解得 BG=6
| 3 |
∴CG=BG-BC=6
| 3 |
∴当x=6
| 3 |
(ii)
∵BC∥OA
∴
| OH′ |
| BG′ |
| OQ |
| BQ |
∵OQ=
| 1 |
| 3 |
∴
| OQ |
| BQ |
| 1 |
| 2 |
∵OH′=OC=3
| 3 |
∴
3
| ||
| BG′ |
| OQ |
| BQ |
| 1 |
| 2 |
解得 BG′=6
| 3 |
∴CG′=BG′+BC=6
| 3 |
∴当x=6
| 3 |
综上所述,x=6
| 3 |
| 3 |
②

如图3,过点M作x轴的平行线l,交GD于N,
由①可得
| OH |
| BG |
| 1 |
| 2 |
∴
| OP |
| BG |
| 1 |
| 2 |
∴2OP+PM=BG+PM.
在Rt△PMN中,
∵PM≥MN(等号在P、N重合时成立)
∴2PO+PM=BG+PM≥BG+MN.
若移动G点至G'位置,此时N',P'重合,此时2PO+PM应最小.
显然G移动,H也跟着移动,圆的大小也发生变化,是否有P、N重合的情景呢?

如图4,在运动的过程中,存在情形使得P、N重合,此时BG+PM=M的横坐标-B的横坐标.
∵B(-3,3
| 3 |
∴2PO+PM=BG+PM=xM-xB=1-(-3)=4,
2PO+PM的最小值是4.
点评:本题考查了等边三角形的特殊性质、圆与直线相切的证明及利用动态图形判断线段何时最短,是一道难度极高的题,尤其(2)②,将倍数线段首先转换并将所求距离转换为两点到直线距离的和,画图及思路不易想到.

练习册系列答案
相关题目
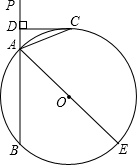 如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,CD为⊙O的切线,C为切点,且CD⊥PA,垂足为D.
如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,CD为⊙O的切线,C为切点,且CD⊥PA,垂足为D.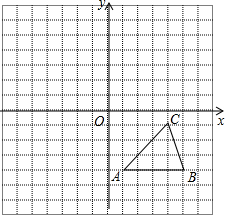 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1). 某种物品包装盒的侧面展开图如图,如果长方体盒子的长比宽多40cm,求这个长方体的体积.
某种物品包装盒的侧面展开图如图,如果长方体盒子的长比宽多40cm,求这个长方体的体积. 如图,在直角坐标系中,O为原点,点A在y轴的正半轴上,∠OAB=90°,B(-5,12),将△ABO绕着点O顺时针旋转90°,使得点A落在点C处,点B落在点D处,联结AD、BD.那么∠ABD的余切值为
如图,在直角坐标系中,O为原点,点A在y轴的正半轴上,∠OAB=90°,B(-5,12),将△ABO绕着点O顺时针旋转90°,使得点A落在点C处,点B落在点D处,联结AD、BD.那么∠ABD的余切值为