题目内容
 已知二次函数y=-x2+2x+3图象的对称轴为直线.
已知二次函数y=-x2+2x+3图象的对称轴为直线.(1)请求出该函数图象的对称轴;
(2)在坐标系内作出该函数的图象;
(3)有一条直线过点P(1,5),若该直线与二次函数y=-x2+2x+3只有一个交点,请求出所有满足条件的直线的关系式.
考点:二次函数的性质,二次函数的图象
专题:
分析:(1)根据对称轴的公式,可得答案;
(2)根据画函数图象的方法,可得抛物线的图象;
(3)根据直线与抛物线相切,可得交点是一个,可得答案.
(2)根据画函数图象的方法,可得抛物线的图象;
(3)根据直线与抛物线相切,可得交点是一个,可得答案.
解答:解:(1)x=-
=-
=1;
(2)图象
(3)因为抛物线的对称轴是x=1,点p(1,5)
当过点p且与y轴平行的直线满足与抛物线只有一个交点
所以直线x=1为所求直线
当过点p的直线不与y轴平行时,设直线的解析式为y=kx+b,
令-x2+2x+3=kx+b
整理得-x2+(2-k)x+3-b=0由题意得△=(2-k)2+4(3-b)=0
即:k2-4k+16-4b=0
又因为y=kx+b,过点p(1,5)
所以5=k+b
所以k2-4=0
解得k=±2,
当k=2时,b=3;
当k=-2时,b=7
所以解析式为y1=2x+3,y2=-2x+7,
所以满足条件的直线有三条:直线x=1;y1=2x+3,y2=-2x+7.
| b |
| 2a |
| 2 |
| 2×(-1) |
(2)图象

(3)因为抛物线的对称轴是x=1,点p(1,5)
当过点p且与y轴平行的直线满足与抛物线只有一个交点
所以直线x=1为所求直线
当过点p的直线不与y轴平行时,设直线的解析式为y=kx+b,
令-x2+2x+3=kx+b
整理得-x2+(2-k)x+3-b=0由题意得△=(2-k)2+4(3-b)=0
即:k2-4k+16-4b=0
又因为y=kx+b,过点p(1,5)
所以5=k+b
所以k2-4=0
解得k=±2,
当k=2时,b=3;
当k=-2时,b=7
所以解析式为y1=2x+3,y2=-2x+7,
所以满足条件的直线有三条:直线x=1;y1=2x+3,y2=-2x+7.
点评:本题考查了二次函数的性质,a<0时,图象开口向下,对称轴是x=-
.
| b |
| 2a |

练习册系列答案
相关题目
 如图,
如图,
 已知:如图,C是AE上一点,∠B=∠DAE,BC∥DE,AC=DE.
已知:如图,C是AE上一点,∠B=∠DAE,BC∥DE,AC=DE. 如图,四边形ABCD是长方形,E为AD上一点,连接BE,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求△DFG的面积.
如图,四边形ABCD是长方形,E为AD上一点,连接BE,其中AB=10,AE=8,ED=4,且F是线段BE的中点,G是线段FC的中点,求△DFG的面积.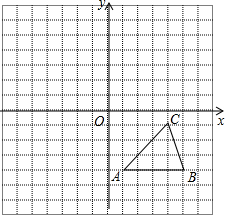 如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).
如图,方格纸中的每个小方格都是边长为1个单位的正方形,在建立平面直角坐标系后,△ABC的顶点均在格点上,点C的坐标为(4,-1).