Question

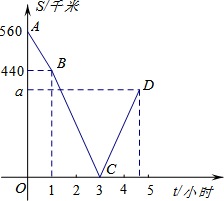甲、乙两车分别从M、N两地相向而行，甲车出发1小时后乙车才出发，并以各自速度匀速行驶，甲车出发3小时两车相遇，相遇后两车仍按原速度原方向各自行驶．如图折线A-B-C-D表示甲、乙两车之间的距离S（千米） 与甲车出发时间t（小时）之间的函数图象．则：
①M、N两地之间的距离为

 

千米；
②当S=50千米时，t=

 

小时．

Answer 1

考点：一次函数的应用

专题：

分析：①根据图象，甲出发时的S值即为M、N两地间的距离；
②先求出甲车的速度，然后设乙车的速度为xkm/h，再利用相遇问题列出方程求解即可；然后求出相遇后甲车到达N地的时间，再根据路程=速度×时间求出两车的相距距离a；
设直线BC的解析式为S=k₁t+b₁（k₁≠0），利用待定系数法求出直线BC的解析式，再令S=50，求出t的值，减去1即为相遇前乙车出发的时间；设直线CD的解析式为S=k₂t+b₂（k₂≠0），利用待定系数法求出直线CD的解析式，再令S=50，求出t的值即为相遇后乙车出发的时间．

解答：解：①t=0时，S=560，
所以，M、N两地的距离为560千米；
②甲车的速度为：（560-440）÷1=120km/h，
设乙车的速度为xkm/h，
则（120+x）×（3-1）=440，
解得x=100；
相遇后甲车到达N地的时间为：（3-1）×100÷120=

5

3

小时，
所以，a=（120+100）×

5

3

=

1100

3

千米；
设直线BC的解析式为S=k₁t+b₁（k₁≠0），
将B（1，440），C（3，0）代入得，

k1+b1=440 3k1+b1=0

，
解得

k1=-220 b1=660

，
所以，S=-220t+660，
当-220t+660=50时，解得t=

61

22

，
直线CD的解析式为S=k₂t+b₂（k₂≠0），
点D的横坐标为

5

3

+3=

14

3

，
将C（3，0），D（

14

3

，

1100

3

）代入得，

3k2+b2=0 14 3 k2+b2= 1100 3

，
解得

k2=220 b2=-660

，
所以，S=220t-660（3≤t≤

14

3

）
当220t-660=50时，解得t=

71

22

，
∴当S=50千米时，t=

61

22

或

71

22

．
故答案为：560；

61

22

或

71

22

．

点评：本题考查了一次函数的应用，主要利用了路程、速度、时间三者之间的关系，准确识图并获取信息是解题的关键，注意要分相遇前和相遇后两种情况讨论．