题目内容
20.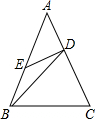 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为( )
| A. | 36° | B. | 45° | C. | 60° | D. | 75° |
分析 根据DE=BE,得到∠EBD=∠EDB=α,根据外角的性质得到∠AED=∠EBD+∠EDB=2α,根据等腰三角形的性质得到∠A=∠AED=2α,于是得到∠BDC=∠A+∠ABD=3α,由于∠ABC=∠C=∠BDC=3α,根据三角形的内角和列方程即可得到结论.
解答 解:∵DE=BE,
∴∠EBD=∠EDB,
设∠EBD=∠EDB=α,
∴∠AED=∠EBD+∠EDB=2α,
∵AD=DE,
∴∠A=∠AED=2α,
∴∠BDC=∠A+∠ABD=3α,
∵BD=BC,AB=AB,
∴∠ABC=∠C=∠BDC=3α,
∴3α+3α+2α=180°,
∴α=22.5°,
∴∠A=45°.
故选:B.
点评 本题考查了等腰三角形的性质,三角形的内角和,三角形的外角的性质,熟练掌握各性质定理是解题的关键.

练习册系列答案
相关题目
11.已知方程6x-9=10x-45与方程3a-1=3(x+a)-2a的解相同.
(1)求这个相同的解;
(2)求a的值;
(3)若[m]表示不大于m的最大整数,求[$\frac{1}{3}$a-2]的值.
(1)求这个相同的解;
(2)求a的值;
(3)若[m]表示不大于m的最大整数,求[$\frac{1}{3}$a-2]的值.
15. 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )| A. | 115° | B. | 120° | C. | 125° | D. | 145° |
 如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.
如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数. 如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹).
如图,已知△ABC,请你在这个三角形内求作一点P,使PA=PB,且点P到边AB、BC的距离也相等(写出作法,保留作图痕迹). 如图,?ABCD中,点E、F分别在AD、BC上,且DE=BF,EF与AC相交于点O,求证:OA=OC.
如图,?ABCD中,点E、F分别在AD、BC上,且DE=BF,EF与AC相交于点O,求证:OA=OC.