题目内容
9. 如图,?ABCD中,点E、F分别在AD、BC上,且DE=BF,EF与AC相交于点O,求证:OA=OC.
如图,?ABCD中,点E、F分别在AD、BC上,且DE=BF,EF与AC相交于点O,求证:OA=OC.
分析 根据ED=BF,可得出AE=CF,结合平行线的性质,可得出∠AEO=∠CFO,∠FCO=∠EAO,继而可判定△AEO≌△CFO,即可得出结论.
解答 证明:∵四边形ABCD是平行四边形,
∴AD=CB,∠AEO=∠CFO,∠FCO=∠EAO,
又∵ED=BF,
∴AD-ED=BC-BF,即AE=CF,
在△AEO和△CFO中,
$\left\{\begin{array}{l}{AE=CF}\\{∠AEO=∠CFO}\\{∠FCO=∠EAO}\end{array}\right.$,
∴△AEO≌△CFO,
∴OA=OC.
点评 此题考查了平行四边形的性质,根据平行四边形的性质得出ED=BF及∠AEO=∠CFO,∠FCO=∠EAO是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | 3a2+a2=4a4 | C. | a2b-ba2=0 | D. | 4a2-5a2=-1 |
20.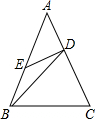 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
BE,那么∠A的度数为( )
 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为( )
| A. | 36° | B. | 45° | C. | 60° | D. | 75° |
17.某食品公司从生产的某批次袋装食品中随机抽出样品20袋,检测每袋的质量是否标准,超过或不足的部分分别用正、负数来表示,记录如表:
(1)这批样品的实际总质量比标准质量相差多少?
(2)若每袋标准质量为450g,则抽样检测的总质量是多少?
(3)若该批次袋装食品共生产了200袋,每袋的质量与标准质量相比,低于2g(不包括2g)则视为不合格,请估算一下该批次袋装食品不合格的袋数有多少?
| 与标准质量的差值(单位g) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 2 | 3 | 4 | 5 | 2 | 4 |
(2)若每袋标准质量为450g,则抽样检测的总质量是多少?
(3)若该批次袋装食品共生产了200袋,每袋的质量与标准质量相比,低于2g(不包括2g)则视为不合格,请估算一下该批次袋装食品不合格的袋数有多少?
4.如果代数式3-x|m|-1+(m+1)x是关于x的二次三项式,那么m的值为( )
| A. | ±3 | B. | 1 | C. | -1 | D. | 2 |
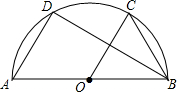 已知:如图,$\widehat{AB}$是半圆,O为AB中点,C,D两点在$\widehat{AB}$上,且AD∥OC,连接BC,BD.$\widehat{CD}$所对的圆心角为60°,求证:$\widehat{AD}$=$\widehat{CD}$.
已知:如图,$\widehat{AB}$是半圆,O为AB中点,C,D两点在$\widehat{AB}$上,且AD∥OC,连接BC,BD.$\widehat{CD}$所对的圆心角为60°,求证:$\widehat{AD}$=$\widehat{CD}$.