题目内容
15. 如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )
如图,将Rt△ABC(其中∠B=30°,∠C=90°)绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,那么旋转角等于( )| A. | 115° | B. | 120° | C. | 125° | D. | 145° |
分析 先利用互余计算出∠BAC=60°,再根据旋转的性质得到∠BAB′等于旋转角,然后利用邻补角计算∠BAB′的度数即可.
解答 解:∵∠B=30°,∠C=90°,
∴∠BAC=60°,
∵Rt△ABC绕点A按顺时针方向旋转到△AB1C1的位置,使得点C、A、B1在同一条直线上,
∴∠BAB1等于旋转角,且∠BAB1=180°-∠BAC=120°,
∴旋转角等于120°.
故选B.
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
5.下面计算正确的是( )
| A. | 6a-5a=1 | B. | a+2a2=3a2 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
20.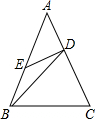 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
BE,那么∠A的度数为( )
 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为( )
| A. | 36° | B. | 45° | C. | 60° | D. | 75° |
4.如果代数式3-x|m|-1+(m+1)x是关于x的二次三项式,那么m的值为( )
| A. | ±3 | B. | 1 | C. | -1 | D. | 2 |
 如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b.
如图所示,点A、点B、点C分别表示有理数a、b、c,O为原点,化简:|a-c|-|b-c|=2c-a-b.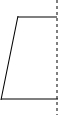 一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考:
一些立体图形可由一些平面图形绕一条直线旋转而得到,这样的几何体叫旋转体,试思考: