题目内容
10. 如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.
如图,已知在△ABC中,AB=AC,BD是∠ABC的角平分线,且BD=BE,∠A=100°,试求∠DEC的度数.
分析 根据等腰三角形的性质及三角形的内角和定理可求出∠ABC,根据角平分线的定义可求出∠DBE,再根据等腰三角形的性质及三角形的内角和定理可求出∠DEB,根据平角的定义就可求出∠DEC的度数.
解答 解:∵AB=AC,
∴∠ABC=∠C=$\frac{1}{2}$(180°-∠A)=$\frac{1}{2}$(180°-100°)=40°.
∵BD是∠ABC的角平分线,
∴∠DBE=$\frac{1}{2}$∠ABC=20°.
∵BD=DE,
∴∠DEB=∠BDE=$\frac{1}{2}$(180°-∠DBE)=$\frac{1}{2}$(180°-20°)=80°.
∴∠DEC=180°-80°=100°.
点评 本题主要考查了等腰三角形的性质、三角形的内角和定理、角平分线的定义、平角的定义等知识,属于基础题,应熟练掌握.

练习册系列答案
相关题目
5.下面计算正确的是( )
| A. | 6a-5a=1 | B. | a+2a2=3a2 | C. | -(a-b)=-a+b | D. | 2(a+b)=2a+b |
19.下列计算正确的是( )
| A. | 2x+3y=5xy | B. | 3a2+a2=4a4 | C. | a2b-ba2=0 | D. | 4a2-5a2=-1 |
20.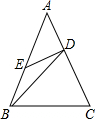 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
BE,那么∠A的度数为( )
 如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=
如图,在△ABC中,AB=AC,D为AC上一点,E为AB上一点,且BC=BD,AD=DE=BE,那么∠A的度数为( )
| A. | 36° | B. | 45° | C. | 60° | D. | 75° |
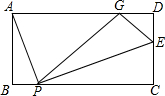 如图,在矩形ABCD中,AB=2,BC=4,P为BC上一点,且和B,C不重合,过P作PE⊥PA交CD所在直线于E,将△PEC沿EP翻折至△PEG,点G正好落在AD上.求PB的长.
如图,在矩形ABCD中,AB=2,BC=4,P为BC上一点,且和B,C不重合,过P作PE⊥PA交CD所在直线于E,将△PEC沿EP翻折至△PEG,点G正好落在AD上.求PB的长. 如图所示,热气球与水平面AB的距离CD=30米,在A处观察热气球的仰角为30°,在B处观察热气球的仰角为45°,求AB之间的距离是多少?(结果保留根号)
如图所示,热气球与水平面AB的距离CD=30米,在A处观察热气球的仰角为30°,在B处观察热气球的仰角为45°,求AB之间的距离是多少?(结果保留根号)