题目内容
(1)如图①,△ABC中,点D、E在边BC上,AD平分∠BAC,AE⊥BC,∠B=35°,∠C=65°,求∠DAE的度数;
(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?

(2)如图②,若把(1)中的条件“AE⊥BC”变成“F为DA延长线上一点,FE⊥BC”,其它条件不变,求∠DFE的度数;
(3)若把(1)中的条件“AE⊥BC”变成“F为AD延长线上一点,FE⊥BC”,其它条件不变,请画出相应的图形,并求出∠DFE的度数;
(4)结合上述三个问题的解决过程,你能得到什么结论?

考点:三角形内角和定理,三角形的外角性质
专题:计算题
分析:(1)根据三角形内角和定理得到∠BAC=180°-∠B-∠C=80°,再利用角平分线定义得∠BAD=
∠BAC=40°,然后计算出∠BAE=90°-∠B=55°,再利用∠DAE=∠BAE-∠BAD进行计算即可;
(2)、(3)作AH⊥BC于H,由(1)得∠DAH=15°,然后利用平行线的性质得到∠DFE=∠ADH=15°;
(4)回答∠BAC角平分线与BC边上的高线平行的直线的夹角为15°即可.
| 1 |
| 2 |
(2)、(3)作AH⊥BC于H,由(1)得∠DAH=15°,然后利用平行线的性质得到∠DFE=∠ADH=15°;
(4)回答∠BAC角平分线与BC边上的高线平行的直线的夹角为15°即可.
解答:解:(1)∠BAC=180°-∠B-∠C=180°-35°-65°=80°,
∵AD平分∠BAC,
∴∠BAD=
∠BAC=40°,
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°-∠B=55°,
∴∠DAE=∠BAE-∠BAD=55°-40°=15°;
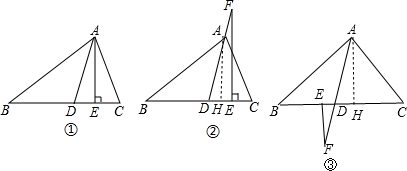 (2)作AH⊥BC于H,如图②,
(2)作AH⊥BC于H,如图②,
有(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠ADH=15°;
(3)作AH⊥BC于H,如图③,
有(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠ADH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
∵AD平分∠BAC,
∴∠BAD=
| 1 |
| 2 |
∵AE⊥BC,
∴∠AEB=90°,
∴∠BAE=90°-∠B=55°,
∴∠DAE=∠BAE-∠BAD=55°-40°=15°;
 (2)作AH⊥BC于H,如图②,
(2)作AH⊥BC于H,如图②,有(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠ADH=15°;
(3)作AH⊥BC于H,如图③,
有(1)得∠DAH=15°,
∵FE⊥BC,
∴AH∥EF,
∴∠DFE=∠ADH=15°;
(4)结合上述三个问题的解决过程,得到∠BAC的角平分线与角平分线上的点作BC的垂线的夹角为15°.
点评:本题考查了三角形内角和定理:三角形内角和是180°.也考查了平行线的性质.

练习册系列答案
相关题目
如果
=-|b-2|,那么以a,b为边长的等腰三角形的周长为( )
| a-5 |
| A、9或12 | B、7或9 |
| C、9 | D、12 |
下列根式属于最简二次根式的是( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知ab=1,M=
,N=
+
,则M与N的关系为( )
| 1 |
| 1+b |
| a |
| 1+a |
| b |
| 1+b |
| A、M>N | B、M=N |
| C、M<N | D、不能确定. |
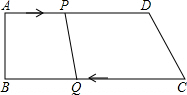 如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=32,点P从A点出发,以1cm/s的速度向D运动,点Q从C点同时出发,以3cm/s的速度向B运动,规定其中一个动点到达端点时,另一个动点,也随之停止运动.
如图,在四边形ABCD中,AD∥BC,∠B=90°,AB=8,AD=24,BC=32,点P从A点出发,以1cm/s的速度向D运动,点Q从C点同时出发,以3cm/s的速度向B运动,规定其中一个动点到达端点时,另一个动点,也随之停止运动. 如图,在?ABCD中,已知对角线AC、BD相交于点O.
如图,在?ABCD中,已知对角线AC、BD相交于点O. 如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′的度数.
如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,求∠AED′的度数.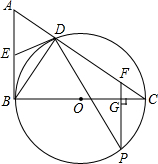 如图,在Rt△ABC中,∠ABC=90°,以BC为直径的⊙O与AC相交于点D,点E为AB的中点,点P是⊙O上一点,过点P作PF⊥BC交BC于点G,交AC于点F.
如图,在Rt△ABC中,∠ABC=90°,以BC为直径的⊙O与AC相交于点D,点E为AB的中点,点P是⊙O上一点,过点P作PF⊥BC交BC于点G,交AC于点F.