题目内容
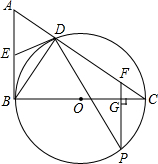如图，在Rt△ABC中，∠ABC=90°，以BC为直径的⊙O与AC相交于点D，点E为AB的中点，点P是⊙O上一点，过点P作PF⊥BC交BC于点G，交AC于点F．（1）试判断ED与⊙O的位置关系并说明理由．
（2）连接CP，若CF=1，CP=2，sinA=
| 4 |
| 5 |
考点：切线的判定,相似三角形的判定与性质
专题：
分析：（1）连接DO，利用圆周角定理得出，△BDC为直角三角形，进而得出∠OBD+∠ABD=90°，求出即可；
（2）首先得出△PCF∽△DCP，进而求出CD=
，由sinA=
，得出BC的长．
（2）首先得出△PCF∽△DCP，进而求出CD=
| PC2 |
| CF |
| 4 |
| 5 |
解答：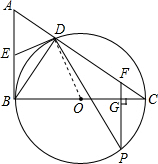
解：（1）ED与⊙O相切．
理由：连接DO，
∵BC为直径，
∴△BDC为直角三角形，
∵OB=OD，
∴∠OBD=∠ODB，
在Rt△ADB中，E为AB中点，
∴DE=BE，
∴∠ABD=∠EDB，
∵∠OBD+∠ABD=90°，
∴ED是⊙O的切线；
（2）∵PF⊥BC，
∴∠FPC=∠PDC，
又∵∠PCF为公共角，
∴△PCF∽△DCP，
∴
=
，
∴CD=
，
又∵CF=1，CP=2，
∴CD=4，
∵sin∠DBC=sinA=
，
∴
=
，
即
=
，
解得：BC=5．
解：（1）ED与⊙O相切．理由：连接DO，
∵BC为直径，
∴△BDC为直角三角形，
∵OB=OD，
∴∠OBD=∠ODB，
在Rt△ADB中，E为AB中点，
∴DE=BE，
∴∠ABD=∠EDB，
∵∠OBD+∠ABD=90°，
∴ED是⊙O的切线；
（2）∵PF⊥BC，
∴∠FPC=∠PDC，
又∵∠PCF为公共角，
∴△PCF∽△DCP，
∴
| PC |
| DC |
| CF |
| CP |
∴CD=
| PC2 |
| CF |
又∵CF=1，CP=2，
∴CD=4，
∵sin∠DBC=sinA=
| 4 |
| 5 |
∴
| DC |
| BC |
| 4 |
| 5 |
即
| 4 |
| BC |
| 4 |
| 5 |
解得：BC=5．
点评：此题主要考查了相似三角形的判定与性质以及圆周角定理和切线的判定等知识，得出CD的长是解题关键．
练习册系列答案
特高级教师点拨系列答案
相关题目
如图，AB=AC，AE是△ABC中BC边上的高线，点D在直线AE上一点（不与A、E重合）．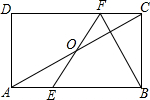
如图，在矩形ABCD中，E、F分别是边AB、CD上的点，AE=CF，EF与对角线AC交于O点．