题目内容
12.已知:x2+2x-7=0,那么$\frac{1}{3}$x2+$\frac{2}{3}$x-5=-$\frac{8}{3}$.分析 观察题中的两个代数式,可以把x2+2x看成一个整体,求得x2+2x的值后,代入所求代数式求值即可得解.
解答 解:∵x2+2x-7=0,
∴x2+2x=7,
∴$\frac{1}{3}$x2+$\frac{2}{3}$x-5=$\frac{1}{3}$(x2+2x)-5=$\frac{7}{3}$-5=-$\frac{8}{3}$,
故答案为-$\frac{8}{3}$
点评 本题考查代数式求值的知识,代数式中的字母表示的数没有明确告知,而是隐含在题设中,首先应从题设中获取代数式x2+2x的值,然后利用“整体代入法”求代数式的值.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.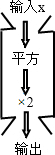 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )
 如图是一组数值转换机,若它输出的结果为32,则输入值为( )
如图是一组数值转换机,若它输出的结果为32,则输入值为( )| A. | ±8 | B. | 8 | C. | ±4 | D. | 4 |
4.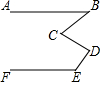 如图,AB∥EF,则下列关系中正确的是( )
如图,AB∥EF,则下列关系中正确的是( )
 如图,AB∥EF,则下列关系中正确的是( )
如图,AB∥EF,则下列关系中正确的是( )| A. | ∠C=∠B+∠D | B. | ∠D+∠E=180°+∠B | ||
| C. | ∠B+∠D+∠E=180°+∠C | D. | ∠E+∠B=∠C+∠D |
1.已知m-n=-3,那么-2(1-m+n)的值为( )
| A. | -4 | B. | 4 | C. | -8 | D. | 8 |
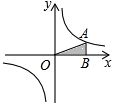 已知图中的曲线为函数y=$\frac{m}{x}$(m为常数,且m≠0)图象的一支.若A为该图象上一点,过点A作AB⊥x轴于点B,当△AOB的面积是2时,m的值为4.
已知图中的曲线为函数y=$\frac{m}{x}$(m为常数,且m≠0)图象的一支.若A为该图象上一点,过点A作AB⊥x轴于点B,当△AOB的面积是2时,m的值为4. 如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长.
如图,在Rt△ABC中,∠A=90°,AB=6,BC=10,D是AC上一点,CD=5,DE⊥BC于E.求线段DE的长.