题目内容
3. 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切.
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切.求⊙C的半径.
分析 首先根据题意作图,由AB是⊙C的切线,即可得CD⊥AB,又由在直角△ABC中,∠C=90°,AC=3,BC=4,根据勾股定理求得AB的长,然后由S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,即可求得以C为圆心与AB相切的圆的半径的长.
解答 解:在△ABC中,
∵AB=5,BC=3,AC=4,
∴AC2+BC2=32+42=52=AB2,
∴∠C=90°,
如图:设切点为D,连接CD,
∵AB是⊙C的切线,
∴CD⊥AB,
∵S△ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CD,
∴AC•BC=AB•CD,
即CD=$\frac{AC•BC}{AB}$=$\frac{3×4}{5}$=$\frac{12}{5}$,
∴⊙C的半径为 $\frac{12}{5}$,
点评 此题考查了圆的切线的性质,勾股定理,以及直角三角形斜边上的高的求解方法.此题难度不大,解题的关键是注意辅助线的作法与数形结合思想的应用.

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
18.某超市在50天内试销一款成本40元/件的新型商品,了解到此款商品第x天的销售信息如下表:
(1)当第5或45天时,该商品的销售单价为65元/件;
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
| 销售量P(件) | p=120-2x |
| 销售单价q(元/件) | 当1≤x<25时,q=x+60; 当25≤x≤50时,q=40+$\frac{1125}{x}$ |
(2)设该商品的利润为W(元),试求W与x的函数关系式;
(3)这50天,该超市哪一天获得的利润W(元)最大?最大利润是多少?
8.下列关于菱形、矩形的说法正确的是( )
| A. | 菱形的对角线相等且互相平分 | B. | 矩形的对角线相等且互相平分 | ||
| C. | 对角线互相垂直的四边形是菱形 | D. | 对角线相等的四边形是矩形 |
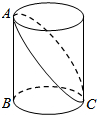 如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )
如图,已知BC是圆柱底面的直径,AB是圆柱的高,在圆柱的侧面上,过点A,C嵌有一圈路径最短的金属丝,现将圆柱侧面沿AB剪开,所得的圆柱侧面展开图是( )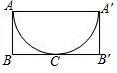
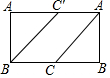
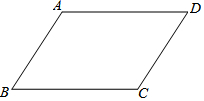 如图,在平行四边形ABCD中,AB<BC.
如图,在平行四边形ABCD中,AB<BC.