题目内容
13.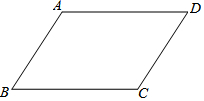 如图,在平行四边形ABCD中,AB<BC.
如图,在平行四边形ABCD中,AB<BC.(1)利用尺规作图,在AD边上确定点E,使点E到边AB,BC的距离相等(不写作法,保留作图痕迹);
(2)若BC=8,CD=5,则DE=3.
分析 (1)作∠ABC的平分线交AD于E,则利用角平分线的性质可得到点E满足条件;
(2)利用平行线的性质和角平分线的定义可证明∠ABE=∠AEB,则AB=AE=5,然后计算AD-AE即可.
解答 解:(1)如图,点E为所作;
(2)由作法得BE平分∠ABC,
∴∠ABE=∠CBE,
∵四边形ABCD为平行四边形,
∴AD∥BC,AD=BC=8,AB=CD=5,
∴∠CBE=∠AEB,
∴∠ABE=∠AEB,
∴AB=AE=5,
∴DE=AD-AE=8-5=3.
故答案为3.
点评 本题考查了作图-基本作图:熟练掌握基本作图(作一条线段等于已知线段;作一个角等于已知角;作已知线段的垂直平分线;作已知角的角平分线;过一点作已知直线的垂线).也考查了平行四边形的性质.

练习册系列答案
相关题目
5.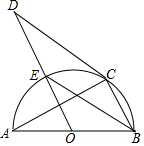 如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
 如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )| A. | AC⊥BC | B. | BE平分∠ABC | C. | BE∥CD | D. | ∠D=∠A |
 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切.
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切.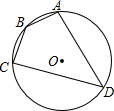 如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.
如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.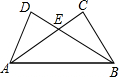 已知:如图,AD=BC,AC=BD.猜想AE与BE的数量关系并证明.
已知:如图,AD=BC,AC=BD.猜想AE与BE的数量关系并证明. 如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为($\sqrt{5}$,2).
如图,在平面直角坐标系中,菱形ABCD的顶点C与原点O重合,点B在y轴的正半轴上,点A在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,点D的坐标为($\sqrt{5}$,2).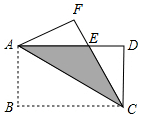 如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.
如图,将矩形ABCD沿对角线AC翻折,点B落在点F处,FC交AD于E.