题目内容
15.为迎接暑假旅游高峰的到来,某旅游纪念品商店决定购进A、B两种纪念品.若购进A种纪念品7件,B种纪念品4件,需要760元;若购进A种纪念品5件.B种纪念品8件,需要800元.(1)求购进A、B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件.考虑市场需求和资金周转,这100件纪念品的资金不少于7000元,但不超过7200元,那么该商店共有几种进货方案?
(3)若销售A种纪念品每件可获利润30元,B种纪念品每件可获利润20元,用(2)中的进货方案,哪一种方案可获利最大?最大利润是多少元?
分析 (1)设购进A种纪念品每件需要x元,购进B种纪念品每件需要y元,根据购买商品的数量及价格之间的关系建立方程组求出其解即可;
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,根据条件中的不相等关系建立不等式组求出其解即可;
(3)设总利润为W元,根据总利润=A种纪念品的利润+B种纪念品的利润就可以表示出W与a的关系式,由一次函数的性质求出其解即可.
解答 解:(1)设购进A种纪念品每件需要x元,购进B种纪念品每件需要y元,由题意,得
$\left\{\begin{array}{l}{7x+4y=760}\\{5x+8y=800}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=80}\\{y=50}\end{array}\right.$.
答:进A种纪念品每件需要80元,购进B种纪念品每件需要50元;
(2)设该商店购进A种纪念品a件,则购进B种纪念品(100-a)套,由题意,得
$\left\{\begin{array}{l}{80a+50(100-a)≥7000}\\{80a+50(100-a)≤7200}\end{array}\right.$,
解得:66$\frac{2}{3}$≤a≤73$\frac{1}{3}$.
∵a为整数,
∴a=67,68,69,70,71,72,73.
∴该商店共有7种进货方案;
(3)设总利润为W元,由题意,得
W=30a+20(100-a)=10a+2000.
∴k=10>0,
∴W随x的增大而增大,
∴该商店购进A种纪念品73件,购进B种纪念品27套,W最大=10×73+2000=2730元.
点评 本题考查了列二元一次方程组解实际问题的运用,列一元一次不等式组解实际问题的运用,一次函数的解析式的运用,解答时由销售问题的数量关系建立方程或不等式是关键.

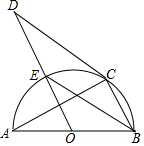 如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )
如图,AB是半圆O的直径,C是半圆O上一点,CD是⊙O的切线,OD∥BC,OD与半圆O交于点E,则下列结论中不一定正确的是( )| A. | AC⊥BC | B. | BE平分∠ABC | C. | BE∥CD | D. | ∠D=∠A |
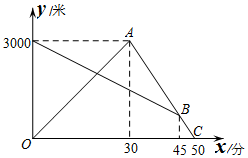 某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米.
某天早晨,小刚从家跑步去体育场锻炼,同时妈妈从体育场晨练结束回家,途中两人相遇,小刚跑到体育场后发现要下雨,立即以另一速度按原路返回,遇到妈妈后,妈妈立即以小刚返回的速度和小刚一起回家(妈妈与小刚行进的路线相同).如图是两人离家的距离y(米)与小刚出发的时间x(分)之间的函数图象,则小刚第一次和妈妈相遇时,妈妈离家的距离为2000 米. 如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是9.
如图,矩形ABCD的对角线AC,BD相交于点O,分别过点C,D作BD,AC的平行线,相交于点E.若AD=6,则点E到AB的距离是9. 如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切.
如图,在△ABC中,AB=5,BC=3,AC=4,以点C为圆心的圆与AB相切. 如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.
如图,直线m∥n,∠1=70°,∠2=30°,则∠A=40°.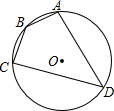 如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.
如图,四边形ABCD内接于⊙O,⊙O的半径为3,∠B=140°,则弧AC的长为$\frac{4}{3}$π.