题目内容
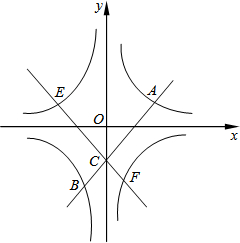 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=| 1 |
| x |
| -1 |
| x |
| 1 |
| x |
| -1 |
| x |
考点:反比例函数综合题
专题:综合题
分析:将A横坐标代入反比例y=
中,求出y的值确定出A的纵坐标,将A坐标代入y=kx+b中表示出b,得到一次函数解析式,与反比例解析式联立,消去y得到关于x的一元二次方程,求出方程的解表示出B坐标,由双曲线y=
与y=-
与直线y=kx+b以及新直线的对称性可得:点A与点E关于y轴对称,点B与点F关于y轴对称,表示出E与F坐标,进而确定出AE与BF,且AE与BF的距离为k+1,利用梯形的面积公式表示出梯形AEBF的面积即可.
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
解答: 解:∵xA=1,A点在y=
解:∵xA=1,A点在y=
上,
∴yA=1,
把点A(1,1)代入y=kx+b中得:1=k+b,
∴b=1-k,
∴y=kx+(1-k),
由
,消去y得:
=kx+(1-k),
整理得:kx2+(1-k)x-1=0,
∴x1=1,x2=-
,
∴点B的坐标为(-
,-k),
由双曲线y=
与y=-
与直线y=kx+b以及新直线的对称性可得:
点A与点E关于y轴对称,点B与点F关于y轴对称,
∴E(-1,1)、F(
,-k),
∴AE=2,BF=
,AE与BF的距离为k+1,
∴S梯形AEBF=
(k+1)=(1+
)(k+1)=k+
+2.
 解:∵xA=1,A点在y=
解:∵xA=1,A点在y=| 1 |
| x |
∴yA=1,
把点A(1,1)代入y=kx+b中得:1=k+b,
∴b=1-k,
∴y=kx+(1-k),
由
|
| 1 |
| x |
整理得:kx2+(1-k)x-1=0,
∴x1=1,x2=-
| 1 |
| k |
∴点B的坐标为(-
| 1 |
| k |
由双曲线y=
| 1 |
| x |
| 1 |
| x |
点A与点E关于y轴对称,点B与点F关于y轴对称,
∴E(-1,1)、F(
| 1 |
| k |
∴AE=2,BF=
| 2 |
| k |
∴S梯形AEBF=
2+
| ||
| 2 |
| 1 |
| k |
| 1 |
| k |
点评:此题属于反比例函数综合题,涉及的知识有:待定系数法确定函数解析式,一次函数与反比例函数的交点,坐标与图形性质,以及对称的性质,由双曲线y=
与y=-
与直线y=kx+b以及新直线的对称性可得:点A与点E关于y轴对称,点B与点F关于y轴对称是解本题的关键.
| 1 |
| x |
| 1 |
| x |

练习册系列答案
 同步奥数系列答案
同步奥数系列答案
相关题目
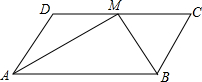 如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )
如图,在平行四边形ABCD中,M是CD的中点,AB=2BC,BM=a,AM=b,则CD的长为( )A、
| ||
B、a+
| ||
C、
| ||
D、
|
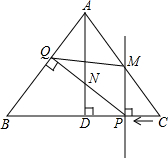 已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题:
已知,如图,在△ABC中,AB=AC=10cm,BC=12cm,AD⊥BC于D,直线PM从点C出发沿CB方向匀速运动,速度为1cm/s;运动过程中始终保持PM⊥BC,直线PM交BC于P,交AC于点M;过点P作PQ⊥AB,交AB于Q,交AD于点N,连接QM,设运动时间是t(s)(0<t<6),解答下列问题: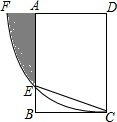 如图,在矩形ABCD中,AD=2
如图,在矩形ABCD中,AD=2