题目内容

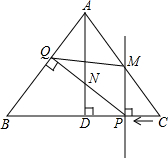已知，如图，在△ABC中，AB=AC=10cm，BC=12cm，AD⊥BC于D，直线PM从点C出发沿CB方向匀速运动，速度为1cm/s；运动过程中始终保持PM⊥BC，直线PM交BC于P，交AC于点M；过点P作PQ⊥AB，交AB于Q，交AD于点N，连接QM，设运动时间是t（s）（0＜t＜6），解答下列问题：
（1）当t为何值时，QM∥BC？
（2）设四边形ANPM的面积为y（cm2），试求出y与t的函数关系式；
（3）是否存在某一时刻t，使y的值最大？若存在，求出t的值；若不存在，请说明理由；
（4）是否存在某一时刻t，使点M在线段PQ的垂直平分线上？若存在，求出t的值；若不存在，请说明理由．
考点：相似形综合题
专题：
分析：（1）QM∥BC，可以得到△BQP∽△QPM，∴QP2=BP•QM，CP=t，AB=AC=10cm，BC=12cm，利用三角函数的比值即可以求得答案．
（2））由△PND∽△BQP∽△ABD，得到
BD
AD
=
DN
PD
，即：
6
8
=
DN
6-t
，∴DN=
18-3t
4
，同理，PM=
4t
3
，根据四边形的面积等于△ACD的面积-△PDN的面积-△PCM的面积可以得到答案．
（3）由（2）的解析式，求顶点坐标可以得到答案．
（4）若点M在线段PQ的垂直平分线上，则MQ=MP，构造关于t的方程，得到答案．
解答：解：（1）因为QM∥BC，
∴△BQP∽△QPM，
∴QP2=BP•QM，∠B=∠QPM，
∵AB=AC=10cm，BC=12cm，AD⊥BC于D，
∴CD=BD=6cm，=8cm，sinB=
QP
BP
=
QM
QP
=
8
10
=
4
5
，
又∵CP=t，
∴BP=12-t，
∴QP=
48-4t
5
，QM=
192-16t
25
，
∴(
48-4t
5
)2=(12-t)(
192-16t
25
)，
解得：t=
54
17
．

（2）∵△PND∽△BQP∽△ABD，
∴
BD
AD
=
DN
PD
，
即：
6
8
=
DN
6-t
，
∴DN=
18-3t
4
，
同理，PM=
4t
3
，
所以y=
1
2
×6×8-
1
2
(6-t)•
18-3t
4
-
1
2
t•
4
3
t=-
25
24
t2+
9
2
t+
21
2


（3）由y=-
25
24
t2+
9
2
t+
21
2
=-
25
24
(x-
54
25
)2+
384
25
，
所以当t=
54
25
时存在最大值．

（4）若点M在线段PQ的垂直平分线上，
则有MQ=MP，
由（1）（2）知道，QM=
192-16t
25
，PM=
4t
3
，
所以
192-16t
25
=
4t
3
，
解得：t=4．
点评：本题考查了相似三角形的判定和性质的综合应用，以及和二次函数结合求最值的方法，学会综合知识的运用是解题的关键．
练习册系列答案
相关题目
一个正方形的面积是10，估计它的边长大小在（　　）
A、2和3之间
B、3和4之间
C、4和5之间
D、5和6之间
解方程时，把某个式子看做整体，用新的未知数去代替它，使方程得到简化，这叫换元法，先阅读下面的解题过程，再解后面的方程：
例：解方程 2
x
-3=0
解：设
x
=t，（t≥0）
∴原方程可化为2t-3=0                
∴t=
3
2
，∴
x
=
3
2
，x=
9
4
．
请利用前面的方法，解方程
x+2
x
-8=0．
如图，在?ABCD中，AE⊥BC于点E，AF⊥DC于F，∠EAF=60°，BE=
3
cm，FD=3cm，求?ABCD的周长．
已知抛物线y=-x2+2mx-m2+1与x轴交点为A、B（点B在点A的右侧），与y轴交于点C．
（1）试用含m的代数式表示A、B两点的坐标；
（2）当点B在原点的右侧，点C在原点的下方时，若△BOC是等腰三角形，求抛物线的解析式；
（3）已知一次函数y=kx+b，点P（n，0）是x轴上一个动点，在（2）的条件下，过点P作垂直于x轴的直线交这个一次函数的图象于点M，交抛物线y=-x2+2mx-m2+1于点N，若只有当1＜n＜4时，点M位于点N的下方，求这个一次函数的解析式．
如图，在平面直角坐标系中，双曲线y=
1
x
与一次函数y=kx+b（k＞0）分别交于点A与点B，直线与y轴交于点C，把直线AB绕着点C旋转一定的角度后，得到一条新直线．若新直线与双曲线y=
-1
x
相交于点E、F，并使得双曲线y=
1
x
，y=
-1
x
，连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称，如果点A的横坐标为1，则点A、点E、点B、点F构成的四边形的面积是多少？（用含k的代数式表示）
观察下列等式：
①
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1；
②
1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2
；
③
1
4
+
3
=
4
-
3
(
4
+
3
)(
4
-
3
)
=
4
-
3
；
…
回答下列问题：
（1）仿照上列等式，写出第n个等式：
 
；
（2）利用你观察到的规律，化简：
1
2
3
+
11
；
（3）计算：
1
1+
2
+
1
2
+
3
+
1
3
+2
+…+
1
3+
10
．
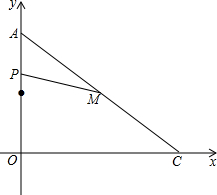如图，在平面直角坐标系中，A（0，6），C（8，0），点M是AC的中点，点P从点A出发，沿着AO→OC的折线运动到C点停止．当以点A，M，P为顶点的三角形是等腰三角形时，直接写出点P的坐标，并写出相应的tan∠APM的值．
先化简，再求值：（
4xy
x-2y
+x）÷
x2+4xy+4y2
4y3-x2y
，其中x、y满足
x=
1
2
y
x-3y=-5
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网