题目内容
(1)解方程:2x2-4x-3=0;
(2)解不等式组
.
(2)解不等式组
|
考点:解一元一次不等式组,解一元二次方程-公式法
专题:
分析:(1)根据公式法求出x的值即可;
(2)分别求出各不等式的解集,再求出其公共解集即可.
(2)分别求出各不等式的解集,再求出其公共解集即可.
解答:解:(1)∵方程2x2-4x-3=0中,x=2,b=-4,c=-3,
∴△=16-(-4)×2×(-3)=40,
∴x=
=
=1±
,即x1=1+
,x2=1-
;
(2)
,
由①得:x<2
由②得x≥-1,
故此不等式组的解集为:-1≤x≤2.
∴△=16-(-4)×2×(-3)=40,
∴x=
4±
| ||
| 4 |
4±2
| ||
| 4 |
| ||
| 2 |
| ||
| 2 |
| ||
| 2 |
(2)
|
由①得:x<2
由②得x≥-1,
故此不等式组的解集为:-1≤x≤2.
点评:本题考查的是解一元一次不等式组,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.

练习册系列答案
相关题目
已知点P(2-4m,m-2)在第二象限,则m的取值范围是( )
A、m>
| ||
| B、m<2 | ||
| C、m>2 | ||
D、
|
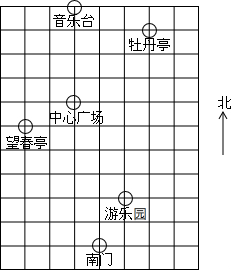 春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m)
春天到了,七(2)班组织同学到公园春游,张明、李华对着景区示意图,如下描述牡丹园位置(图中小正方形边长代表100m) 如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于F,∠EAF=60°,BE=
如图,在?ABCD中,AE⊥BC于点E,AF⊥DC于F,∠EAF=60°,BE=
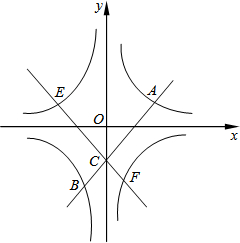 如图,在平面直角坐标系中,双曲线y=
如图,在平面直角坐标系中,双曲线y=