题目内容

当k为何值时，关于x、y的二元一次方程组
2x-3y=5
x+y=k
的解满足x≤y？
考点：二元一次方程组的解,解一元一次不等式
专题：计算题
分析：将k看做已知数表示出x与y，代入不等式即可求出k的范围．
解答：解：
2x-3y=5①
x+y=k②
，
①+②×3得：5x=3k+5，即x=
3k+5
5
，
将x=
3k+5
5
代入②得：y=k-
3k+5
5
，
代入不等式得：
3k+5
5
≤k-
3k+5
5
，
去分母得：3k+5≤5k-3k-5，
解得：k≤10．
点评：此题考查了二元一次方程组的解，方程组的解即为能使方程组中两方程成立的未知数的值．
练习册系列答案
相关题目
如图，在直角三角形中，两直角边长为a，b斜边上的高为h，判断以ab，ah，bh为边长的三角形形状并说明理由．
如图，在?ABCD中，AE⊥BC于点E，AF⊥DC于F，∠EAF=60°，BE=
3
cm，FD=3cm，求?ABCD的周长．
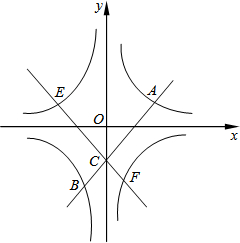如图，在平面直角坐标系中，双曲线y=
1
x
与一次函数y=kx+b（k＞0）分别交于点A与点B，直线与y轴交于点C，把直线AB绕着点C旋转一定的角度后，得到一条新直线．若新直线与双曲线y=
-1
x
相交于点E、F，并使得双曲线y=
1
x
，y=
-1
x
，连线y=kx+b以及新直线构成的图形能关于某条坐标轴对称，如果点A的横坐标为1，则点A、点E、点B、点F构成的四边形的面积是多少？（用含k的代数式表示）
观察下列等式：
①
1
2
+1
=
2
-1
(
2
+1)(
2
-1)
=
2
-1；
②
1
3
+
2
=
3
-
2
(
3
+
2
)(
3
-
2
)
=
3
-
2
；
③
1
4
+
3
=
4
-
3
(
4
+
3
)(
4
-
3
)
=
4
-
3
；
…
回答下列问题：
（1）仿照上列等式，写出第n个等式：
 
；
（2）利用你观察到的规律，化简：
1
2
3
+
11
；
（3）计算：
1
1+
2
+
1
2
+
3
+
1
3
+2
+…+
1
3+
10
．
已知△ABC中，AB=AC，CD⊥AB于D．若AB=10，CD=6，求BD的长．
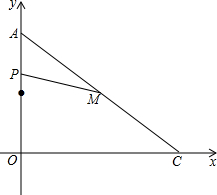如图，在平面直角坐标系中，A（0，6），C（8，0），点M是AC的中点，点P从点A出发，沿着AO→OC的折线运动到C点停止．当以点A，M，P为顶点的三角形是等腰三角形时，直接写出点P的坐标，并写出相应的tan∠APM的值．
计算：
（1）(
1
2
)-2-(
3
-
2
)0+2sin60°-|-3|；
（2）（x-2）（x+1）-（x-1）2．
已知方程
x
x-5
=3-
a
x-5
有增根，则a的值为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网