题目内容
已知抛物线经过A（0，-3）、B（2，-3）、C（4，5），判断点D（-2，5）是否在该抛物线上．你的
结论是： （填“是”或“否”）．
结论是：
考点：二次函数图象上点的坐标特征
专题：计算题
分析：利用点A与点B的坐标特征得到抛物线的对称轴为直线x=1，然后根据抛物线的对称性可判断点C（4，5与点D（-2，5）是抛物线上的对称点．
解答：解：∵抛物线经过A（0，-3）、B（2，-3），
而点A与点B关于直线x=1对称，
∴抛物线的对称轴为直线x=1，
∴点C（4，5）关于直线x=1的对称点D（-2，5）在抛物线上．
故答案为：是．
而点A与点B关于直线x=1对称，
∴抛物线的对称轴为直线x=1，
∴点C（4，5）关于直线x=1的对称点D（-2，5）在抛物线上．
故答案为：是．
点评：本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．也考查了抛物线的对称性．
练习册系列答案
阅读快车系列答案
相关题目
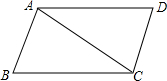如图，在四边形ABCD中，AD∥BC，如果添加下列条件，不能使得△ABC∽△DCA成立的是（ ）| A、∠BAC=∠ADC | ||||
| B、∠B=∠ACD | ||||
| C、AC2=AD•BC | ||||
D、
|
抛物线y=（m-1）x2-mx-m2+1的图象过原点，则m的值为（ ）
| A、±1 | B、0 | C、1 | D、-1 |
已知反比例函数y=
的图象在第二、四象限，则a的取值范围是（ ）
| a-2 |
| x |
| A、a＜2 | B、a＞2 |
| C、a≤2 | D、a≥2 |
如图，直线y=-2x+8与两坐标轴分别交于P、Q两点，在线段PQ上有一点A，过A点分别作两坐标轴的垂线，垂足分别为B、C．