题目内容
抛物线y=(m-1)x2-mx-m2+1的图象过原点,则m的值为( )
| A、±1 | B、0 | C、1 | D、-1 |
考点:二次函数图象上点的坐标特征,二次函数的定义
专题:计算题
分析:根据二次函数图象上点的坐标特征得到-m2+1=0,解得m1=1,m2=-1,然后根据二次函数的定义确定m的值.
解答:解:把(0,0)代入y=(m-1)x2-mx-m2+1得-m2+1=0,解得m1=1,m2=-1,
而m-1≠0,
所以m=-1.
故选D.
而m-1≠0,
所以m=-1.
故选D.
点评:本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了二次函数的定义.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
⊙O的半径为5cm,弦AB∥CD,且AB=8cm,CD=6cm,则AB与CD之间的距离为( )
| A、1cm |
| B、7cm |
| C、3cm或4cm |
| D、1cm或7cm |
一个圆锥模型,它的底面半径为1,高为2
,则这个圆锥的侧面积是( )
| 2 |
| A、4π | ||
| B、3π | ||
C、2
| ||
| D、2π |
下列各组数中互为相反数的是( )
| A、(-2)3与-23 | ||
B、2与
| ||
| C、-1与(-1)2 | ||
| D、2与|-2| |
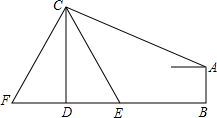 如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.
如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.