题目内容
求下列二次函数与x轴的交点:
(1)y=x2+4x-5
(2)y=-x2+x+2
(3)y=x2-3x
(4)y=x2-6x+10.
(1)y=x2+4x-5
(2)y=-x2+x+2
(3)y=x2-3x
(4)y=x2-6x+10.
考点:抛物线与x轴的交点
专题:
分析:(1)根据抛物线与x轴的交点问题,解方程x2+4x-5=0即可得到二次函数与x轴的交点坐标;
(2)、(3)与(1)一样求解;
(4)根据抛物线与x轴的交点问题,解方程x2-6x+10=0,△<0,于是可判断抛物线与x轴没有交点.
(2)、(3)与(1)一样求解;
(4)根据抛物线与x轴的交点问题,解方程x2-6x+10=0,△<0,于是可判断抛物线与x轴没有交点.
解答:解:(1)当y=0时,x2+4x-5=0,解得x1=-5,x2=1,
所以二次函数与x轴的交点坐标为(-5,0),(1,0);
(2)当y=0时,-x2+x+2=0,解得x1=-1,x2=2,
所以二次函数与x轴的交点坐标为(-1,0),(2,0);
(3)当y=0时,x2-3x=0,所以二次函数与x轴的交点坐标为(0,0),(3,0);
(4)当y=0时,x2-6x+10=0,△=(-6)2-4×10=-4<0,
所以二次函数与x轴没有交点.
所以二次函数与x轴的交点坐标为(-5,0),(1,0);
(2)当y=0时,-x2+x+2=0,解得x1=-1,x2=2,
所以二次函数与x轴的交点坐标为(-1,0),(2,0);
(3)当y=0时,x2-3x=0,所以二次函数与x轴的交点坐标为(0,0),(3,0);
(4)当y=0时,x2-6x+10=0,△=(-6)2-4×10=-4<0,
所以二次函数与x轴没有交点.
点评:本题考查了抛物线与x轴的交点:求二次函数y=ax2+bx+c(a,b,c是常数,a≠0)与x轴的交点坐标,令y=0,即ax2+bx+c=0,解关于x的一元二次方程即可求得交点横坐标.△=b2-4ac决定抛物线与x轴的交点个数:△=b2-4ac>0时,抛物线与x轴有2个交点;△=b2-4ac=0时,抛物线与x轴有1个交点;△=b2-4ac<0时,抛物线与x轴没有交点.

练习册系列答案
相关题目
 一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是
一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是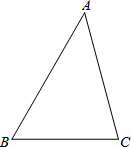 如图,△ABC中,∠B=60°,∠C=75°,AC=
如图,△ABC中,∠B=60°,∠C=75°,AC=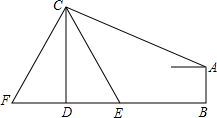 如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长.
如图,在电线杆上的C处引拉线CE、CF固定电线杆.拉线CE和地面成60°角,在离电线杆6米处安置测角仪AB,在A处测得电线杆上C处得仰角为23°,已知测角仪AB的高为1.5米,求拉线CE的长. 我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足:
我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足: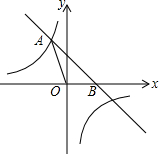 如图,直线y=-x+2与反比例函数y=
如图,直线y=-x+2与反比例函数y=