题目内容
已知二次函数y=-2x2+bx+c的图象经过点A(0,4)和B(1,-2).
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
(1)求此函数的解析式;并运用配方法,将此抛物线解析式化为y=a(x+m)2+k的形式;
(2)写出该抛物线顶点C的坐标,并求出△CAO的面积.
考点:二次函数的三种形式
专题:
分析:(1)将A(0,4)和B(1,-2)代入y=-2x2+bx+c求得b,c的值,得到此函数的解析式;再利用配方法先提出二次项系数,然后加上一次项系数的一半的平方来凑完全平方式,把一般式转化为顶点式;
(2)由顶点式可得顶点C的坐标,再根据三角形的面积公式即可求出△CAO的面积.
(2)由顶点式可得顶点C的坐标,再根据三角形的面积公式即可求出△CAO的面积.
解答:解:(1)将A(0,4)和B(1,-2)代入y=-2x2+bx+c,
得
,
解得
,
所以此函数的解析式为y=-2x2-4x+4;
y=-2x2-4x+4=-2(x2+2x+1)+2+4=-2(x+1)2+6;
(2)∵y=-2(x+1)2+6,
∴C(-1,6),
∴△CAO的面积=
×4×1=2.
得
|
解得
|
所以此函数的解析式为y=-2x2-4x+4;
y=-2x2-4x+4=-2(x2+2x+1)+2+4=-2(x+1)2+6;
(2)∵y=-2(x+1)2+6,
∴C(-1,6),
∴△CAO的面积=
| 1 |
| 2 |
点评:本题考查了用待定系数法求二次函数的解析式,二次函数解析式的三种形式,二次函数的性质以及三角形的面积,难度适中.正确求出函数的解析式是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
下列计算结果正确的是( )
| A、(-a3)2=a9 | ||
| B、a2•a3=a6 | ||
C、(
| ||
D、(cos60°-
|
某农家前年水蜜桃的亩产量为800千克,今年的亩产量为1200千克.假设从前年到今年水蜜桃亩产量的年平均增长率都为x,则可列方程( )
| A、800(1+2x)=1200 |
| B、800(1+x2)=1200 |
| C、800(1+x)2=1200 |
| D、800(1+x)=1200 |
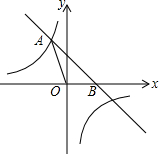 如图,直线y=-x+2与反比例函数y=
如图,直线y=-x+2与反比例函数y=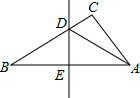 如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )cm.
如图,△ABC中边AB的垂直平分线分别交BC、AB于点D、E,AE=3cm,△ADC的周长为9cm,则△ABC的周长是( )cm. 如图,直径AB=6的半圆,绕B点顺时针旋转60°,此时点A就到了点A′,则图中阴影部分的面积是
如图,直径AB=6的半圆,绕B点顺时针旋转60°,此时点A就到了点A′,则图中阴影部分的面积是