题目内容
在平面直角坐标系xOy中,点A(-2,n)在反比例函数y=-
的图象上,AB⊥x轴于点B,那么△AOB的面积等于 .
| 6 |
| x |
考点:反比例函数系数k的几何意义
专题:计算题
分析:直接根据反比例函数比例系数k的几何意义求解.
解答:解:∵AB⊥x轴于点B,
∴△AOB的面积=
×|-6|=3.
故答案为3.

∴△AOB的面积=
| 1 |
| 2 |
故答案为3.
点评:本题考查了反比例函数比例系数k的几何意义:在反比例函数y=xk图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是
|k|,且保持不变.
| 1 |
| 2 |

练习册系列答案
相关题目
如果把Rt△ABC的三边长度都扩大2倍,那么锐角A的四个三角比的值( )
| A、都扩大到原来的2倍 | ||
B、都缩小到原来的
| ||
| C、都没有变化 | ||
| D、都不能确定 |
某农家前年水蜜桃的亩产量为800千克,今年的亩产量为1200千克.假设从前年到今年水蜜桃亩产量的年平均增长率都为x,则可列方程( )
| A、800(1+2x)=1200 |
| B、800(1+x2)=1200 |
| C、800(1+x)2=1200 |
| D、800(1+x)=1200 |
 一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是
一名射击运动员连续打靶8次,命中的环数如图所示,这组数据的中位数是 我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足:
我们定义:如果一个图形上的点A′、B′、…、P′和另一个图形上的点A、B、…、P 分别对应,并且满足: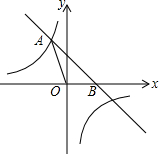 如图,直线y=-x+2与反比例函数y=
如图,直线y=-x+2与反比例函数y=