题目内容
16. 如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).
如图,矩形ABCD中,AB=16cm,BC=6cm,点P从点A出发沿AB向点B移动(不与点A、B重合),一直到达点B为止;同时,点Q从点C出发沿CD向点D移动(不与点C、D重合).(1)若点P、Q均以3cm/s的速度移动,经过多长时间四边形BPDQ为菱形?
(2)若点P为3cm/s的速度移动,点Q以2cm/s的速度移动,经过多长时间△DPQ为直角三角形?
分析 (1)根据矩形的性质可得出AB∥CD,再由点P、Q移动的速度相同即可得出四边形BPDQ是平行四边形,如要四边形BPDQ是菱形只需BP=DP,设经过xs,四边形BPDQ是菱形,用x表示出BP、DP,由此即可得出关于x的一元二次方程,解方程即可得出结论;
(2)由∠PDQ≠90°可知△DPQ为直角三角形分两种情况.①当∠DPQ=90°时,过点Q作QM⊥AB于M,利用勾股定理即可得出关于x的一元二次方程,解方程即可求出x值;②当∠DQP=90°时,则AP+CQ=16,由此可得出关于x的一元一次方程,解方程即可得出x值.综上即可得出结论.
解答 解:(1)∵四边形ABCD是矩形,
∴AB∥CD.
∵点P、Q均以3cm/s的速度移动,
∴AP=CQ,
∴BP=DQ,
∴四边形BPDQ是平行四边形,
∴当BP=DP时,四边形BPDQ是菱形.
设经过xs,四边形BPDQ是菱形,则有AP=3xcm,BP=(16-3x)cm,
由勾股定理得:DP2=(3x)2+62,
∴DP2=(3x)2+62=(16-3x)2,
解得:x=$\frac{55}{24}$.
答:经过$\frac{55}{24}$s时四边形BPDQ是菱形.
(2)∵点P不与点A重合,
∴∠PDQ≠90°,
∴△DPQ为直角三角形分两种情况:
①当∠DPQ=90°时,△DPQ为直角三角形,过点Q作QM⊥AB于M,易得四边形BCQM为矩形,如图所示.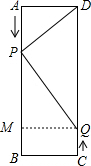
∵AP=3xcm,BM=CQ=2xcm,则PM=(16-5x)cm,DQ=(16-2x)cm,
∴(16-5x)2+62+(3x)2+62=(16-2x)2,
解得:x1=2,x2=$\frac{6}{5}$;
②当∠DQP=90°时,AP+CQ=16,
所以3x+2x=16,解得:x=$\frac{16}{5}$.
综上可知:经过2s、$\frac{6}{5}$s或$\frac{16}{5}$s时,△DPQ为直角三角形.
点评 本题考查了矩形的性质、勾股定理得逆定理以及菱形的判定,解题的关键是:(1)根据邻边相等找出关于x的一元二次方程;(2)分两种情况考虑.本题属于中档题,难度不大,解决该题型题目时,根据菱形的判定、勾股定理得逆定理得出关于x的方程是关键.

| A. | 2000 | B. | 2000名考生 | ||
| C. | 54988名考生的数学成绩 | D. | 2000名考生的数学成绩 |
| A. | 有公共顶点的两个角是对顶角 | |
| B. | 多项式x2-4x因式分解的结果是x(x2-4) | |
| C. | a+a=a2 | |
| D. | 一元二次方程x2-x+2=0无实数根 |
 如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形.现用Ai表示第三行开始,从左往右,从上往下,依次出现的第i个数,例如:A1=1,A2=2,A3=1,A4=1,A5=3,A6=3,A7=1,则A2016=1953.
如图所示的三角形数组是我国古代数学家杨辉发现的,称为杨辉三角形.现用Ai表示第三行开始,从左往右,从上往下,依次出现的第i个数,例如:A1=1,A2=2,A3=1,A4=1,A5=3,A6=3,A7=1,则A2016=1953.