题目内容
如图将两个正方形的一个顶点重合放置，若∠AOD=40°，则∠COB=考点：余角和补角
专题：
分析：根据正方形各角等于90°，得出∠COD+∠AOB=180°，再根据∠AOD=40°，∠COB=∠COD+∠AOB-∠AOD，即可得出答案．
解答：解：∵两个图形是正方形，
∴∠COD=90°，∠AOB=90°，
∴∠COD+∠AOB=180°，
∵∠AOD=40°，
∴∠COB=∠COD+∠AOB-∠AOD=140°．
故答案为：140．
∴∠COD=90°，∠AOB=90°，
∴∠COD+∠AOB=180°，
∵∠AOD=40°，
∴∠COB=∠COD+∠AOB-∠AOD=140°．
故答案为：140．
点评：此题考查了角的计算，用到的知识点是余角和补角，根据所给出的图形，找到角与角的关系是本题的关键．
练习册系列答案
相关题目
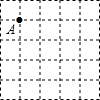在5×5的正方形方格中，每个小正方形的边长都为1，请在下图给定的网格中按下列要求画出图形．
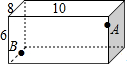如图所示，在长、宽、高分别为10cm、8cm、6cm的长方体器皿的A点（三等分点）有一只蚂蚁，在B点（四等分点）处有一粒大米，请计算：蚂蚁要吃到大米最少要走多远．已知⊙O的半径为7cm，OA=5cm，那么点A与⊙O的位置关系是（ ）
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
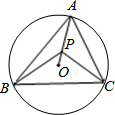如图，⊙O是△ABC的外接圆，∠BAC=55°，点P在半径AO上（不与A，O重合），则∠BPC可能为数轴上到原点的距离等于1的点所表示的数是（ ）
| A、±1 | B、0 | C、1 | D、-1 |