题目内容
设A(-2,y1),B(1,y2),C(2,y3)是抛物线y=(x+1)2+a上的三点,则y1,y2,y3的大小关系为 .(用>号连接)
考点:二次函数图象上点的坐标特征
专题:
分析:先求出抛物线对称轴,再根据点A、B、C与对称轴的距离的大小与二次函数的增减性解答.
解答:解:抛物线y=(x+1)2+a的对称轴是直线x=-1,
∵抛物线开口向上,点A、B、C到对称轴的距离分别为1、2、3,
∴y3>y2>y1.
故答案为:y3>y2>y1.
∵抛物线开口向上,点A、B、C到对称轴的距离分别为1、2、3,
∴y3>y2>y1.
故答案为:y3>y2>y1.
点评:本题考查了二次函数图象上点的坐标特征,主要利用了二次函数的增减性,求出对称轴解析式是解题的关键.

练习册系列答案
相关题目
下列方程中,是关于x的一元二次方程的是( )
A、
| ||||
| B、ax2+bx+c=0 | ||||
| C、x2+2x=x2-1 | ||||
| D、3(x+1)2=2(x+1) |
 由10个边长为1的小正方体搭成一个几何体,其俯视图如图,则该几何体主视图和左视图的面积和不可能是( )
由10个边长为1的小正方体搭成一个几何体,其俯视图如图,则该几何体主视图和左视图的面积和不可能是( )| A、9 | B、13 | C、14 | D、17 |
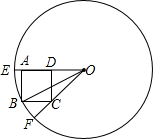 如图,已知圆O的直径为10cm,圆上有三点E、B、F,四边形ABCD为正方形,∠EOF=45°,求AB的长度?
如图,已知圆O的直径为10cm,圆上有三点E、B、F,四边形ABCD为正方形,∠EOF=45°,求AB的长度? 如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=
如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=