题目内容

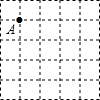在5×5的正方形方格中，每个小正方形的边长都为1，请在下图给定的网格中按下列要求画出图形．
（1）从点A出发，画一条线段AB，使它的另一个端点B在格点（小正方形的每个顶点都称为格点）上，且长度为2
2
．
（2）画出所有以（1）中AB为边的等腰三角形，使另一个顶点在格点上，且另两边的长度都是无理数，并写出所有满足条件的三角形．
考点：勾股定理,无理数,等腰三角形的判定
专题：网格型
分析：（1）根据勾股定理可知使线段AB为边长为2的等腰直角三角形的斜边即可；
（2）作AB的垂直平分线和网格相交并且满足边长为无理数即可．
解答：解：（1）如图所示：

（2）如图所示：
点评：本题考查了勾股定理、垂直平分线的性质，熟知勾股定理的定义是解答此题的关键．
练习册系列答案
相关题目
代数式
2x+1
中x的取值范围是（　　）
A、x＞-
1
2
B、x≥
1
2
C、x＞
1
2
D、x≥-
1
2
用四舍五入法将2.5979精确到百分位得到的近似数是
 
．
如图，直线AB分别交双曲线y=
k
x
及y=
1
x
的第一象限的图象于A，B两点，直线CD分别交双曲线y=
k
x
及y=
1
x
的第一图象的图象于C，D两点，AB∥CD∥y轴，AB=2CD，且四边形ABCD的面积为
9
4
，则k的值为
 
．
如图，两个直角梯形重叠在一起，将梯形ABCD沿AD方向平移至梯形EFGH，求阴影部分的面积．（单位：cm）
如图，O为直线AB与直线CF的交点，∠BOC=α．
（1）如图1所示，若α=40°，OD平分∠AOC，∠DOE=90°，求∠EOF的度数；
（2）如图2所示，若∠AOD=
1
4
∠AOC，∠DOE=45°，试求∠EOF的度数；（注意：∠BOC=α）
（3）如图3所示，若∠AOD=
1
n
∠AOC，∠DOE=
180°
n
，n≥2，且n为正整数，猜想∠EOF与α的数量关系是
 
（直接写出结果，不要求写过程）
下列方程中，是关于x的一元二次方程的是（　　）
A、
1
x2
+
1
x
-2=0
B、ax2+bx+c=0
C、x2+2x=x2-1
D、3（x+1）2=2（x+1）
【新概念定义】若有一条公共边的两个三角形称为“共边三角形”．如图（1）△ABC与△ABD是以AB为公共边的
“共边三角形”．“共边三角形”的性质：如图（1）共边△ABC与△ABD，连结第三个顶点DC并延长交AB于E，则
S△ABC
S△ABD
=
CE
DE
．
【问题解决】
如图（2），已知在△ABC中，D为BC的中点，E为AD的中点，BE的连线交AC于F．
（1）找出以BF为公共边的所有“共边三角形”，若△ABC的面积为45cm2，分别求出这些“共边三角形”的面积；
（2）求证：AF=
1
3
AC；
（3）若将“D为BC的中点”条件，改为“BD：DC=2：3”．则
AF
CF
=
 
．
如图将两个正方形的一个顶点重合放置，若∠AOD=40°，则∠COB=
 
 度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网