题目内容
已知⊙O的半径为7cm,OA=5cm,那么点A与⊙O的位置关系是( )
| A、在⊙O内 | B、在⊙O上 |
| C、在⊙O外 | D、不能确定 |
考点:点与圆的位置关系
专题:
分析:要确定点与圆的位置关系,主要确定点与圆心的距离与半径的大小关系;利用d>r时,点在圆外;当d=r时,点在圆上;当d<r时,点在圆内判断出即可.
解答:解:∵⊙O的半径为7cm,OA=5cm,
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故选A.
∴d<r,
∴点A与⊙O的位置关系是:点A在圆内,
故选A.
点评:此题主要考查了对点与圆的位置关系的判断.关键要记住若半径为r,点到圆心的距离为d,则有:当d>r时,点在圆外;当d=r时,点在圆上,当d<r时,点在圆内.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
下列方程中,是关于x的一元二次方程的是( )
A、
| ||||
| B、ax2+bx+c=0 | ||||
| C、x2+2x=x2-1 | ||||
| D、3(x+1)2=2(x+1) |
过一个正多边形的某个顶点的所有对角线,将这个正多边形分成了4个三角形,则这个正多边形的每一个内角的度数是( )
| A、120° | B、90° |
| C、60° | D、30° |
已知等腰三角形其中两边的长分别是8和6,第三边的长是一元二次方程x2-16x+60=0的一个实数根,则该三角形的周长是( )
| A、20 | B、24 |
| C、24或20 | D、无法确定 |
 如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=
如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB= 如图,圆柱的底面半径为6cm,高为10cm,蚂蚁在圆柱表面爬行.从点A爬到点B的最短路程是多少厘米(结果保留小数点后一位)?
如图,圆柱的底面半径为6cm,高为10cm,蚂蚁在圆柱表面爬行.从点A爬到点B的最短路程是多少厘米(结果保留小数点后一位)?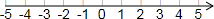 我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:
我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题: