题目内容
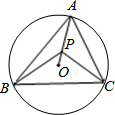 如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为
如图,⊙O是△ABC的外接圆,∠BAC=55°,点P在半径AO上(不与A,O重合),则∠BPC可能为考点:圆周角定理
专题:开放型
分析:首先连接OB与OC,由∠BAC=55°,根据同弧所对圆周角等于其所对圆心角的一半,即可求得∠BOC的度数,又由∠BAC<∠BPC<∠BOC,即可求得答案.
解答: 解:连接OB与OC,
解:连接OB与OC,
∵⊙O是△ABC的外接圆,∠BAC=55°,
∴∠BOC=2∠BAC=110°,
∵∠BAC<∠BPC<∠BOC,
∴55°<∠BPC<110°.
故答案为:70 (答案不唯一,大于55小于110都可).
 解:连接OB与OC,
解:连接OB与OC,∵⊙O是△ABC的外接圆,∠BAC=55°,
∴∠BOC=2∠BAC=110°,
∵∠BAC<∠BPC<∠BOC,
∴55°<∠BPC<110°.
故答案为:70 (答案不唯一,大于55小于110都可).
点评:此题考查了圆周角定理.此题难度不大,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
过一个正多边形的某个顶点的所有对角线,将这个正多边形分成了4个三角形,则这个正多边形的每一个内角的度数是( )
| A、120° | B、90° |
| C、60° | D、30° |
 由5个相同的正方体搭成的几何体如图所示,则它的左视图是( )
由5个相同的正方体搭成的几何体如图所示,则它的左视图是( )A、 |
B、 |
C、 |
D、 |
 如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=
如图将两个正方形的一个顶点重合放置,若∠AOD=40°,则∠COB=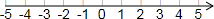 我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题:
我们知道:|a|的几何意义可以理解为数轴上表示数a的点与原点之间的距离,请大家运用相关知识继续探索数轴上多个点之间的距离问题: 如图所示,A点表示-4.
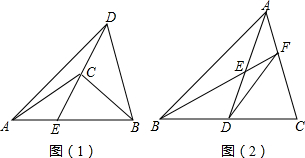
如图所示,A点表示-4. 如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB垂直平分线分别交AB,AC及BC的延长线于点D,E,F,求CE和CF的长.
如图,在Rt△ABC中,∠C=90°,AC=12,BC=9,AB垂直平分线分别交AB,AC及BC的延长线于点D,E,F,求CE和CF的长.