题目内容
20.(1)计算:-22+$\sqrt{9}$-2cos60°+($\frac{1}{3}$)-1;(2)在Rt△ABC中,∠C=90°,若sinA=$\frac{12}{13}$,求cosB,tanB的值.
分析 (1)分别根据数的乘方及开方法则、特殊角的三角函数值及负整数指数幂的计算法则分别计算出各数,再根据实数混合运算的法则进行计算即可;
(2)根据题意画出图形,根据sinA=$\frac{12}{13}$可设BC=12x,则AB=13x,根据勾股定理求出AC的长,再由锐角三角函数的定义即可得出结论.
解答 解:(1)原式=-4+3-2×$\frac{1}{2}$+3
=-4+3-1+3
=1; (2)如图所示,∵∠C=90°,sinA=$\frac{12}{13}$,
(2)如图所示,∵∠C=90°,sinA=$\frac{12}{13}$,
∴设BC=12x,则AB=13x,
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{169x}^{2}-{144x}^{2}}$=5x,
∴cosB=$\frac{BC}{AB}$=$\frac{12x}{13x}$=$\frac{12}{13}$,tanB=$\frac{AC}{AB}$=$\frac{5x}{13x}$=$\frac{5}{13}$.
点评 本题考查的是实数的运算,熟知数的乘方及开方法则、特殊角的三角函数值及负整数指数幂的计算法则是解答此题的关键.

练习册系列答案
相关题目
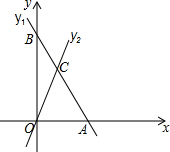 如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).
如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).