题目内容
5.现有5个质地均匀的小球上分别标有数字-1,-2,1,2,3,将标有数字-2,1,3的小球放在第一个不透明的盒子里,再将其余小球放在另个不透明的盒子里;现分别从两个盒子里各摸出一个小球,将小球上的数字作为m、n的值,并代入方程:mx2+3x+n=0中.(1)请利用列表或画树状图的方法表示取出的两个小球上的数字之积所有可能的结果;
(2)求摸出两球上的数字能使方程:mx2+3x+n=0有实数解的概率;
(3)选一组摸出的m,n的值代入方程:mx2+3x+n=0中,设它的解为x1、x2,求x21+x22的值.
分析 (1)首先根据题意列出表格,由表格即可求得取出的两个小球上数字之积所有等可能的结果;
(2)根据(1)中的表格,利用根的判别式计算判定求得答案;
(3)找出一组数值,代入方程,利用根与系数的关系求得数值即可.
解答 解:(1)列表得:
| -1 | 2 | |
| -2 | 2 | -4 |
| 1 | -1 | 2 |
| 3 | -3 | 6 |
(2)mx2+3x+n=0,
△=9-4mn,经检验,2,-4,-1,-3,2这5组数值使方程:mx2+3x+n=0有实数解,
因此P(有实数解)=$\frac{5}{6}$;
(3)取mn=-4,
则-2x2+3x+2=0
x1+x2=$\frac{3}{2}$,x1,x2=-1,
x21+x22=(x1+x2)2-2x1x2=$\frac{9}{4}$+2=$\frac{17}{4}$.
点评 此题考查的是用列表法或树状图法求概率.注意树状图法与列表法可以不重复不遗漏的列出所有可能的结果,一元二次方程根的判别式,一元二次方程根与系数的关系等知识.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
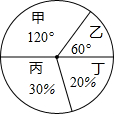 红星中学对今年中考数学成绩进行调研,将其成绩分成三类,其中甲类250人,请你画出条形统计图.
红星中学对今年中考数学成绩进行调研,将其成绩分成三类,其中甲类250人,请你画出条形统计图.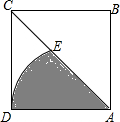 如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.