题目内容
12.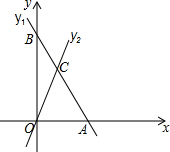 如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).
如图,在平面直角坐标系中,直线y1=kx+b与y2=3x交于点C(a,3),与x轴、y轴分别交于点A,B,点B的坐标为(0,5).(1)求一次函数的表达式;
(2)当y1>y2时,x的取值范围是x<1.(直接写出答案)
分析 (1)把C(a,3)代入y2=3x求得a的值为1,然后把B(0,5),C(1,3)代入y1=kx+b,根据待定系数法即可求得;
(2)由图象可知,当x<1时,函数y1的图象在函数y2的上方.
解答 解:(1)∵直线y1=kx+b与y2=3x交于点C(a,3),
∴3=3a,
∴a=1,
∴C(1,3),
把B(0,5),C(1,3)代入y1=kx+b得$\left\{\begin{array}{l}{b=5}\\{k+b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-2}\\{b=5}\end{array}\right.$.
∴一次函数的表达式为y1=-2x+5;
(2)由图象可知,当y1>y2时,x的取值范围是x<1.
故答案为x<1.
点评 本题考查了两条直线相交问题,交点坐标适合两个解析式是解题的关键.

练习册系列答案
 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
1.下列各式中正确的是( )
| A. | -3(a-7)=-3a-21 | B. | 3a-(4a2+2)=3a-4a2+2 | ||
| C. | -[-(2a+3y)]=2a-3y | D. | -2x-y=-(2x+y) |
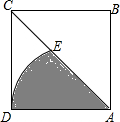 如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.