题目内容
9.已知一次函数的图象与反比例函数的图象的交点为A(-3,1),B(2,n)两点.(1)求点B的坐标;
(2)求一次函数和反比例函数的解析式.
分析 (1)先把A点坐标代入反比例函数y=$\frac{m}{x}$,求出m确定反比例函数解析式为y=-$\frac{3}{x}$;再把B(2,n)代入y=-$\frac{3}{x}$求出n,确定B点坐标;
(2)把A、B的坐标代入一次函数y=kx+b,利用待定系数法确定一次函数解析式;
解答 解:(1)∵A(-3,1),B(2,n)两点是反比例函数图象上的点,
设反比例函数为y=$\frac{m}{x}$,
∴m=-3×1=2n,
∴m=-3,n=-$\frac{3}{2}$,
∴B(2,-$\frac{3}{2}$);
(2)∴m=-3,
∴反比例函数为y=-$\frac{3}{x}$,
设一次函数为y=kx+b,
把A(-3,1)和B(2,-$\frac{3}{2}$)代入y=kx+b得$\left\{\begin{array}{l}{-3k+b=1}\\{2k+b=-\frac{3}{2}}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$.
所以一次函数解析式为y=-$\frac{1}{2}$x-$\frac{1}{2}$.
点评 本题考查了反比例函数与一次函数的交点问题:反比例函数与一次函数图象的交点坐标满足两函数解析式.也考查了待定系数法求函数解析式以及观察函数图象的能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
1.下列各式中正确的是( )
| A. | -3(a-7)=-3a-21 | B. | 3a-(4a2+2)=3a-4a2+2 | ||
| C. | -[-(2a+3y)]=2a-3y | D. | -2x-y=-(2x+y) |
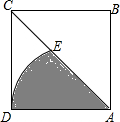 如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长.
如图,正方形ABCD中,以A为圆心,AD为半径作弧交AC于E,若阴影部分的面积为2π,求AC的长. 如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β
如图所示,将一个矩形沿图中的虚线折叠,用量角器测量一下其中的α,β,得α=β