题目内容
16．
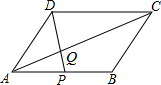如图，在?ABCD中，点P在AB上，连结DP，交AC于点Q，当点P是AB的中点时，△ADQ的面积为1，则?ABCD的面积为（ ）| A． | 3 | B． | 4 | C． | 6 | D． | 12 |
分析 由平行四边形的性质和已知条件得出AB∥CD，AB=CD=2AP，?ABCD的面积=2△ACD的面积，由平行线得出△APQ∽△CDQ，得出AQ：CQ=AP：CD=1：2，求出△CDQ的面积=2，得出△ACD的面积=△ADQ的面积+△CDQ的面积=3，即可得出结果．
解答 解：∵四边形ABCD是平行四边形，点P是AB的中点，
∴AB∥CD，AB=CD=2AP，
∴?ABCD的面积=2△ACD的面积，
∴△APQ∽△CDQ，
∴AQ：CQ=AP：CD=1：2，
∵△ADQ的面积为1，
∴△CDQ的面积=2，
∴△ACD的面积=△ADQ的面积+△CDQ的面积=3，
∴?ABCD的面积=2×3=6；
故选：C．
点评 本题考查了平行四边形的性质、相似三角形的判定与性质、三角形的面积关系；熟练掌握平行四边形的性质，由相似三角形的性质得出AQ：CQ=1：2是解决问题的关键．
练习册系列答案
名校课堂系列答案
相关题目
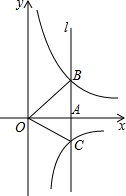如图，经过点A（3，0）的直线l平行于y轴，与双曲线y=$\frac{4}{x}$和y=$\frac{k}{x}$分别交于点B和C．
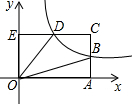如图，反比例函数y=$\frac{k}{x}$（x＞0）的图象交矩形OECA的边AC于B点，交CE于D点，且B是AC的中点，若四边形ODCB的面积是5，则k=5．
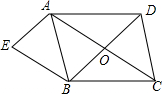如图，在?ABCD中，对角线AC、BD相交于点O，AE∥BD，BE∥AC，AE与BE相交于点E，当AB，AD满足什么条件时，四边形AEBO为矩形？请说明埋由．
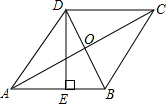如图，在菱形ABCD中，DE=AO，DE⊥AB，AB=2．
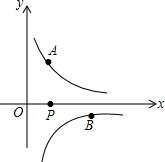如图，已知点A（$\frac{1}{2}$，y1），B（2，y2）分别为反比例函数y=$\frac{1}{x}$，y=$\frac{-1}{x}$图象上的点，动点P在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，P的坐标是（$\frac{5}{2}$，0）．
如图，在?ABCD中，AE=CF，试说明EF，BD互相平分的理由．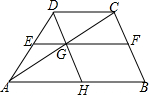
已知：如图，在?BCDH中，G是DH的中点，连接CG，CG与BH的延长线交于点A，连接AD，E是AD的中点，连接EG并延长交BC于点F，求证：GF=2EG．