题目内容
10.在平面直角坐标系中,坐标原点为O,直线l1:y=-x+2与y轴交于点B.直线l2:y=-$\frac{1}{2}$x+b与l1交于点N(点N不与B重合).设△OBN的面积分别为S,当0≤b≤1时,求S关于b的函数关系式,并求出S的最大值.分析 先求出y=-x+2和y=-$\frac{1}{2}$x+b的交点N的坐标,根据三角形的面积公式表示出三角形OBN的面积,根据一次函数的性质求出S的最大值.
解答 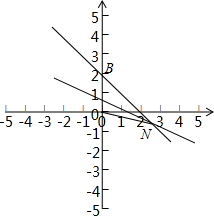 解:y=-x+2与y轴交于点B的坐标(0,2),
解:y=-x+2与y轴交于点B的坐标(0,2),
由题意得,$\left\{\begin{array}{l}{y=-x+2}\\{y=-\frac{1}{2}x+b}\end{array}\right.$,
解得,$\left\{\begin{array}{l}{x=4-2b}\\{y=2b-2}\end{array}\right.$,
则点N的坐标(4-2b,2b-2),
△OBN的面积S=$\frac{1}{2}$×2×(4-2b)=4-2b,
即S=-2b+4,
∵-2<0,
∴S随b的增大而减小,
∴当x=0时,S有最大值4.
点评 本题考查的是两条直线的交点的求法和一次函数的性质,列出二元一次方程组、解方程组求出交点坐标是解题的关键,注意数形结合思想的正确运用.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
15.在平面直角坐标系中,到x轴的距离等于2个单位长度,且到y轴的距离等于3个单位长度的点有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.下列各点,在函数y=2x-3的图象上的是( )
| A. | (1,1) | B. | (-1,5) | C. | (-2,-7) | D. | (-$\frac{3}{2}$,0) |
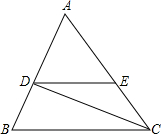 如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为25°.
如图,△ABC中,∠A=60°,∠B=70°,CD是∠ACB的平分线,点E在AC上,DE∥BC,则∠EDC的度数为25°.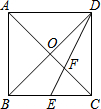 如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.
如图,在边长为2的正方形ABCD中,对角线AC、BD交于点O,E是BC的中点,DE交AC于点F,则EF的长为$\frac{\sqrt{5}}{3}$.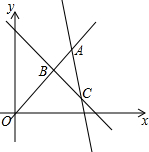 已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.
已知直线y1=x,y2=-3x+16,y3=-x+6的图象如图所示,求△ABC的面积.
 如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.
如图,CD平分∠ACB,且CD∥AE,如果∠ACE=80°.求∠CAE.