题目内容
19.下列各点,在函数y=2x-3的图象上的是( )| A. | (1,1) | B. | (-1,5) | C. | (-2,-7) | D. | (-$\frac{3}{2}$,0) |
分析 把x=1,x=-1,x=-2,x=$-\frac{3}{2}$代入y=2x-3,计算出对应的函数值,然后根据一次函数图象上点的坐标特征判断各点是否在直线y=2x-3上.
解答 解:当x=1时,y=2x-3=-1;当x=-1时,y=2x-3=-5;当x=-2时,y=2x-3=-7;
所以点(-2,-7)在直线y=2x-3上.
故选C
点评 本题考查了一次函数图象上点的坐标特征:直线上任意一点的坐标都满足函数关系式y=kx+b.

练习册系列答案
相关题目
11.对于函数y=$\frac{6}{x}$,下列说法错误的是( )
| A. | 它的图象分布在第一、三象限 | B. | 它的图象与直线y=-x无交点 | ||
| C. | 当x>0时,y的值随x的增大而增大 | D. | 当x<0时,y的值随x的增大而减小 |
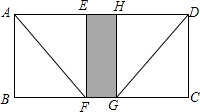 如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm
如图,将长方形纸片ABCD折叠,使得AB与AD重合,点B落在点E处,压平得折痕AF,则四边形ABFE是正方形:再将CD与AD重合,点C落在点H处,压平得折痕DG,则四边形CDHG也是正方形,展开后发现四边形EFGH正好与四边形ABCD相似,量得AB=10cm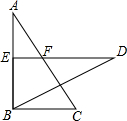 如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60°
如图,已知△ABC≌△DEB,点E在AB上,DE与AC相交于点F,若DE=7,BC=4,∠D=35°,∠C=60° 在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.
在平行四边形ABCD中,AB=$\sqrt{13}$,AD=4,将平行四边形ABCD沿AE翻折后,点B恰好与点C重合,则该平行四边形ABCD的面积为12.