题目内容
5．
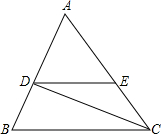如图，△ABC中，∠A=60°，∠B=70°，CD是∠ACB的平分线，点E在AC上，DE∥BC，则∠EDC的度数为25°．
分析 先根据三角形内角和定理求出∠ACB的度数，再由角平分线的性质求出∠BCD的度数，根据平行线的性质即可得出结论．
解答 解：∵△ABC中，∠A=60°，∠B=70°，
∴∠ACB=180°-60°-70°=50°．
∵CD是∠ACB的平分线，
∴∠BCD=$\frac{1}{2}$∠ACB=25°．
∵DE∥BC，
∴∠EDC=∠BCD=25°．
故答案为：25°．
点评 本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键．
练习册系列答案
相关题目
如图，函数y=-x与函数y=-$\frac{4}{x}$的图象交于A，B两点，过A，B两点分别作y轴的垂线，垂足分别为点C，点D．则四边形ACBD的面积为8．
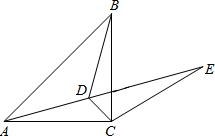如图所示，已知点D为等腰直角三角形ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA，则∠DCE的度数是105°．
一个正方体的表面展开图如图所示，已知这个正方体的每一个面上都填有一个数字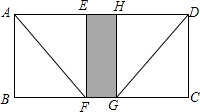
如图，将长方形纸片ABCD折叠，使得AB与AD重合，点B落在点E处，压平得折痕AF，则四边形ABFE是正方形：再将CD与AD重合，点C落在点H处，压平得折痕DG，则四边形CDHG也是正方形，展开后发现四边形EFGH正好与四边形ABCD相似，量得AB=10cm